题目内容
设f(x)=(x+1)ln(x+1)-ax2-x(a∈R)
(Ⅰ)若a=0求函数f(x)的极值点及相应的极值;
(Ⅱ)若对任意x∈(0,+∞),f(x)<0恒成立,求实数a的取值范围.
(Ⅰ)若a=0求函数f(x)的极值点及相应的极值;
(Ⅱ)若对任意x∈(0,+∞),f(x)<0恒成立,求实数a的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)a=0时,f(x)=(x+1)ln(x+1)-x,从而f′(x)=ln(x+1),当x>0时,f′(x)>0,x<0时,f′(x)<0,于是x=0是函数的极小值点,相应的极小值为f(0)=0.
(Ⅱ)f′(x)=ln(x+1)-2ax,设m(x)=f′(x),则m′(x)=
-2a=
,分情况讨论①当a≤0时,②当a<0时从而综合得出结论.
(Ⅱ)f′(x)=ln(x+1)-2ax,设m(x)=f′(x),则m′(x)=
| 1 |
| x+1 |
| -2ax+1-2a |
| x+1 |
解答:
解(Ⅰ)a=0时,f(x)=(x+1)ln(x+1)-x,
∴f′(x)=ln(x+1),
当x>0时,f′(x)>0,x<0时,f′(x)<0,
∴x=0是函数的极小值点,相应的极小值为f(0)=0;
(Ⅱ)f′(x)=ln(x+1)-2ax,
设m(x)=f′(x),
则m′(x)=
-2a=
,
①当a≤0时,m′(x)>0则m(x)=f′(x)在(0,+∞)上为增函数,
∴f′(x)>f′(0)=0,
∴f(x)在(0,+∞)上为增函数,
∴f(x)>f(0)=0与f(x)<0恒成立矛盾.
②当a<0时,m′(x)=-2a
,
若1-2a≤0即a≥
时,m″(x)<0,
则m(x)=f′(x)在(0,+∞)上为减函数,
∴f′(x)<f′(0)=0,
∴f(x)在(0,+∞)上为减函数,
∴f(x)<f(0)=0满足题意.
若1-2a>0,即0<a<
时,若x∈(0,
),则m′(x)>0
则m(x)=f′(x)在(0,
)上为增函数,
从而有f′(x)>f′(0)=0,
∴f(x)在(0,
)上为增函数,
∴f(x)>f(0)=0与f(x)<0恒成立矛盾.
综上所述,实数a的取值范围.是[
,+∞).
∴f′(x)=ln(x+1),
当x>0时,f′(x)>0,x<0时,f′(x)<0,
∴x=0是函数的极小值点,相应的极小值为f(0)=0;
(Ⅱ)f′(x)=ln(x+1)-2ax,
设m(x)=f′(x),
则m′(x)=
| 1 |
| x+1 |
| -2ax+1-2a |
| x+1 |
①当a≤0时,m′(x)>0则m(x)=f′(x)在(0,+∞)上为增函数,
∴f′(x)>f′(0)=0,
∴f(x)在(0,+∞)上为增函数,
∴f(x)>f(0)=0与f(x)<0恒成立矛盾.
②当a<0时,m′(x)=-2a
x-
| ||
| x+1 |
若1-2a≤0即a≥
| 1 |
| 2 |
则m(x)=f′(x)在(0,+∞)上为减函数,
∴f′(x)<f′(0)=0,
∴f(x)在(0,+∞)上为减函数,
∴f(x)<f(0)=0满足题意.
若1-2a>0,即0<a<
| 1 |
| 2 |
| 1-2a |
| 2a |
则m(x)=f′(x)在(0,
| 1-2a |
| 2a |
从而有f′(x)>f′(0)=0,
∴f(x)在(0,
| 1-2a |
| 2a |
∴f(x)>f(0)=0与f(x)<0恒成立矛盾.
综上所述,实数a的取值范围.是[
| 1 |
| 2 |
点评:本题考察了利用导数研究函数的单调性,函数的最值问题,不等式恒成立问题,本题是一道综合题.

练习册系列答案
相关题目
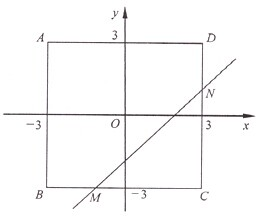 如图,四边形ABCD由不等式组
如图,四边形ABCD由不等式组