题目内容
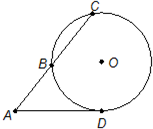如图，从圆O外一点A引圆的切线AD和割线ABC，已知AD=4| 2 |
| 5 |
考点：圆的切线的性质定理的证明
专题：计算题,立体几何
分析：先由切割线定理，得到BC的长，再由半径长、弦心距、半弦长构成的直角三角形，利用勾股定理求出半径的长，运用圆的面积公式即可．
解答：
解：∵AD为圆O的切线，ABC为圆O的割线
由切割线定理得：
AD2=AB•AC
即8AB=（4
）2，
∴AB=4，BC=AC-AB=4，
设圆O的半径为r，
由于圆心O到AC的距离为
，BC=4，
故r2=（
）2+22=9，即r=3，
则圆的面积为9π．
故答案为：9π．
由切割线定理得：
AD2=AB•AC
即8AB=（4
| 2 |
∴AB=4，BC=AC-AB=4，
设圆O的半径为r，
由于圆心O到AC的距离为
| 5 |
故r2=（
| 5 |
则圆的面积为9π．
故答案为：9π．
点评：本题考查弦长公式和切割线定理，本题解题的关键是根据半径长、弦心距、半弦长构成直角三角形，这是圆中常见的一种方法．
练习册系列答案
相关题目
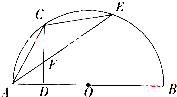如图，半圆O的直径AB的长为4，点C平分弧AE，过C作AB的垂线交AB于D，交AE干F．
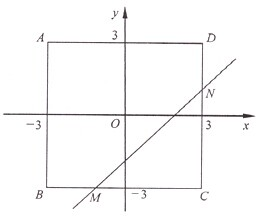如图，四边形ABCD由不等式组