题目内容
已知函数f(x)=sin
-
cos
.
(1)求函数f(x)的周期,最大值和单调递减区间;
(2)若f(x)=(2-
)cos
,求tanx;
(3)在(2)的条件下,求
的值.
| x |
| 2 |
| 3 |
| x |
| 2 |
(1)求函数f(x)的周期,最大值和单调递减区间;
(2)若f(x)=(2-
| 3 |
| x |
| 2 |
(3)在(2)的条件下,求
sin(
| ||||
|
考点:三角函数中的恒等变换应用,运用诱导公式化简求值,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(1)先利用两角和公式对函数解析式化简,根据周期公式求得最小正周期,根据三角函数图象与性质求得函数的最大值和单调增区间.
(2)根据f(x)的解析式,和已知条件建立等式求得tan
的值,进而根据二倍角公式求得tanx的值.
(3)利用tanx的值,分别求得sinxcosx,sin2x和cos2x的值,对原式利用诱导公式和两角和公式化简整理代入即可.
(2)根据f(x)的解析式,和已知条件建立等式求得tan
| x |
| 2 |
(3)利用tanx的值,分别求得sinxcosx,sin2x和cos2x的值,对原式利用诱导公式和两角和公式化简整理代入即可.
解答:
解:(1)f(x)=sin
-
cos
=2(
sin
-
cos
)=2sin(
-
),
∴T=
=4π,f(x)max=2×1=2,
当2kπ+
≤
-
≤2kπ+
时,4kπ+
≤x≤4kπ+
,k∈Z,
即函数的单调减区间为[4kπ+
,4kπ+
](k∈Z).
(2)f(x)=(2-
)cos
=2sin(
-
),
∴sin
=2cos
,
∴tan
=2,
∴tanx=
=
=-
(3)∵tanx=-
,
∴sinxcosx=-
×
=-
,sin2x=(±
)2=
,cos2x=1-2sin2x=1-
=-
.
∴
=
=
=
=-
.
| x |
| 2 |
| 3 |
| x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| ||
| 2 |
| x |
| 2 |
| x |
| 2 |
| π |
| 3 |
∴T=
| 2π | ||
|
当2kπ+
| π |
| 2 |
| x |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| 5π |
| 3 |
| 11π |
| 3 |
即函数的单调减区间为[4kπ+
| 5π |
| 3 |
| 11π |
| 3 |
(2)f(x)=(2-
| 3 |
| x |
| 2 |
| x |
| 2 |
| π |
| 3 |
∴sin
| x |
| 2 |
| x |
| 2 |
∴tan
| x |
| 2 |
∴tanx=
2tan
| ||
1-tan2
|
| 2×2 |
| 1-4 |
| 4 |
| 3 |
(3)∵tanx=-
| 4 |
| 3 |
∴sinxcosx=-
| 3 |
| 5 |
| 4 |
| 5 |
| 12 |
| 25 |
| 4 |
| 5 |
| 16 |
| 25 |
| 32 |
| 25 |
| 7 |
| 25 |
∴
sin(
| ||||
|
| -cos2x | ||||||||||
-
|
| -cos2x |
| -sinxcosx+sin2x |
-
| ||||
|
| 1 |
| 4 |
点评:本题主要考查了三角函数恒等变换的应用,诱导公式的应用,三角函数图象与性质.考查了对学生基础知识的综合运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
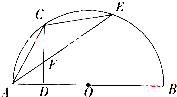 如图,半圆O的直径AB的长为4,点C平分弧AE,过C作AB的垂线交AB于D,交AE干F.
如图,半圆O的直径AB的长为4,点C平分弧AE,过C作AB的垂线交AB于D,交AE干F.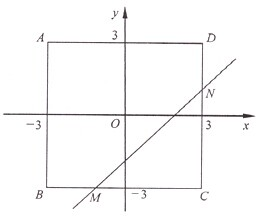 如图,四边形ABCD由不等式组
如图,四边形ABCD由不等式组