题目内容
3.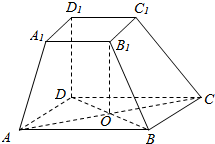 在四棱台ABCD-A1B1C1D1中,D1D⊥ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,∠BAD=60°.
在四棱台ABCD-A1B1C1D1中,D1D⊥ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,∠BAD=60°.(1)求证:BB1⊥AC.
(2)连结AC,BD,设交点O,连结B1O.设AB=2,D1D=2,求三棱锥B1-ABO外接球的体积.
分析 (1)底面平行四边形ABCD中,AB=AD,可得四边形ABCD是菱形,可得AC⊥BD,又DD1⊥平面ABCD,可得DD1⊥AC,因此AC⊥平面BDD1,即可证明.
(2)证明三棱锥B1-ABO的三条侧棱互相垂直,2R=$\sqrt{3+4+1}$=2$\sqrt{2}$,即可求三棱锥B1-ABO外接球的体积.
解答 (1)证明:底面平行四边形ABCD中,连接AC,BD,设AC∩BD=O.
∵AB=AD,∴四边形ABCD是菱形,
∴AC⊥BD,
又DD1⊥平面ABCD,
∴DD1⊥AC,又BD∩DD1=D,
∴AC⊥平面BDD1,
又∵四棱台ABCD-A1B1C1D1中,侧棱DD1与BB1延长后交于一点,
∴BB1?平面BDD1,∴AC⊥BB1.即BB1⊥AC;
(2)解:∵AB=2A1B1,∴BD=2D1B1,
∵BD=2OD,
∴OD=D1B1,
∵OD∥D1B1,
∴四边形B1D1DO是平行四边形,
∴D1D∥B1O,
∵DD1⊥平面ABCD,
∴B1O⊥平面ABCD,
∵AB=AD,四边形ABCD是平行四边形,
∴AO⊥OB,
∴三棱锥B1-ABO的三条侧棱互相垂直,
∴2R=$\sqrt{3+4+1}$=2$\sqrt{2}$,
∴V=$\frac{8\sqrt{2}π}{3}$.
点评 本题考查了证明线面垂直、长方体外接球的体积计算公式、平行四边形与菱形的性质,考查了空间想象能力,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
11.设Sn为等差数列{an}的前n项和,a2=2,S5=15,若$\{\frac{1}{{{a_n}•{a_{n+1}}}}\}$的前n项和为$\frac{9}{10}$,则n的值为( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
15.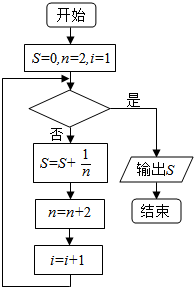 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{96}$的值的一个程序框图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{96}$的值的一个程序框图,其中判断框内应填入的条件是( )
 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{96}$的值的一个程序框图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{96}$的值的一个程序框图,其中判断框内应填入的条件是( )| A. | i>48 | B. | i>24 | C. | i<48 | D. | i<24 |
13.函数f(x)=log0.8(2x2-ax+3)在(-1,+∞)为减函数,则a的范围( )
| A. | (-5,-4] | B. | [-5,-4] | C. | (-∞,-4) | D. | (-∞,-4] |
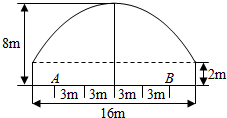 有一隧道,内设双行线公路,同方向有两个车道(共有四个车道),每个车道宽为3m,此隧道的截面由一个长方形和一抛物线构成.如图所示,隧道高8m,宽16m,为了保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方面上高度之差至少为0.25m,靠近中轴线的车道为快车道,两侧的车道为慢车道,求车辆通过隧道时,慢车道的限制高度(用分数表示).
有一隧道,内设双行线公路,同方向有两个车道(共有四个车道),每个车道宽为3m,此隧道的截面由一个长方形和一抛物线构成.如图所示,隧道高8m,宽16m,为了保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方面上高度之差至少为0.25m,靠近中轴线的车道为快车道,两侧的车道为慢车道,求车辆通过隧道时,慢车道的限制高度(用分数表示).