题目内容
18.已知双曲线$\frac{y^2}{16}-\frac{x^2}{20}=1$上一点P到焦点F1的距离等于9,则点P到F2的距离等于17.分析 由双曲线的方程,先求出a=4,再利用双曲线的定义可求.
解答 解:由题意,P在双曲线的左支上,
由双曲线的定义,可得|PF2|-|PF1|=2a=8,
因为|PF1|=9,所以|PF2|=17.
故答案为:17
点评 本题主要考查了双曲线的性质,运用双曲线的定义||PF1|-|PF2||=2a,是解题的关键,属基础题.

练习册系列答案
相关题目
7.已知x>0,y>0,ln3x+ln9y=ln3,则$\frac{2}{x}+\frac{1}{y}$的最小值是( )
| A. | 6 | B. | $6+\sqrt{2}$ | C. | 8 | D. | $4+2\sqrt{2}$ |
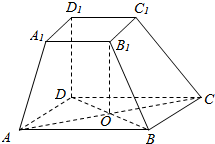 在四棱台ABCD-A1B1C1D1中,D1D⊥ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,∠BAD=60°.
在四棱台ABCD-A1B1C1D1中,D1D⊥ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,∠BAD=60°.