题目内容
13.从抛物线y2=8x上任一点P向x轴作垂线段,垂足为D,求垂线段中点M的轨迹方程.分析 先设出垂线段的中点为M(x,y),P(x0,y0)是抛物线上的点,把它们坐标之间的关系找出来,代入抛物线的方程即可.
解答 解:设M(x,y),P(x0,y0),D(x0,0),
因为M是PD的中点,所以x0=x,y=$\frac{1}{2}$y0,
有x0=x,y0=2y,
因为点P在抛物线上,所以y0=8x0,即4y2=8x,
所以y2=2x,所求点M轨迹方程为:y2=2x.
点评 本题主要考查求轨迹方程的方法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
3.已知平面α截一球面得圆M,过圆心M且与α成30°二面角的平面β截该球面得圆N.若该球面的半径为4,圆M的面积为4π,则圆N的面积为( )
| A. | 7π | B. | 9π | C. | 11π | D. | 13π |
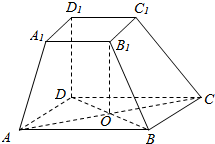 在四棱台ABCD-A1B1C1D1中,D1D⊥ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,∠BAD=60°.
在四棱台ABCD-A1B1C1D1中,D1D⊥ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,∠BAD=60°.