题目内容
13.函数f(x)=log0.8(2x2-ax+3)在(-1,+∞)为减函数,则a的范围( )| A. | (-5,-4] | B. | [-5,-4] | C. | (-∞,-4) | D. | (-∞,-4] |
分析 令t=2x2-ax+3>0,由题意可得函数t在(-1,+∞)上是增函数,且2+a+3≥0,得到$\frac{a}{4}$≤-1,由此解得a的范围.
解答 解:令t=2x2-ax+3>0,由题意可得函数t在(-1,+∞)上是增函数,且2+a+3≥0,
∴$\frac{a}{4}$≤-1,且a≥-5,解得a∈[-5,-4],
故选:B.
点评 本题主要考查复合函数的单调性,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
5.要得到余弦曲线y=cosx,只需将正弦曲线y=sinx向左平移( )
| A. | $\frac{π}{2}$个单位 | B. | $\frac{π}{3}$个单位 | C. | $\frac{π}{4}$个单位 | D. | $\frac{π}{6}$个单位 |
3.三个数0.993,log20.6,log3π的大小关系为( )
| A. | log3π<0.993<log20.6 | B. | log20.6<log3π<0.993 | ||
| C. | 0.993<log20.6<log3π | D. | log20.6<0.993<log3π |
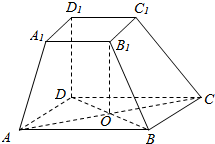 在四棱台ABCD-A1B1C1D1中,D1D⊥ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,∠BAD=60°.
在四棱台ABCD-A1B1C1D1中,D1D⊥ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,∠BAD=60°.