题目内容
12.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的一条渐近线被圆M:x2+y2-8y+15=0截得的弦长为$\sqrt{2}$,则双曲线的离心率为4$\sqrt{2}$.分析 求出双曲线的一条渐近线方程,利用渐近线被圆M:x2+y2-8y+15=0截得的弦长为$\sqrt{2}$,可得$\frac{|0-4a|}{\sqrt{{b}^{2}+{a}^{2}}}$=$\frac{\sqrt{2}}{2}$,即可求出双曲线的离心率.
解答 解:圆M:x2+y2-8y+15=0,可化为x2+(y-4)2=1.圆心(0,4),半径为1.
依题意可知双曲线的一渐近线方程为bx-ay=0,
∵弦长为$\sqrt{2}$,圆的半径为1,
由弦长的一半、半径和圆心到直线的距离构成直角三角形,
则圆心到渐近线的距离d=$\frac{\sqrt{2}}{2}$,
即$\frac{|0-4a|}{\sqrt{{b}^{2}+{a}^{2}}}$=$\frac{\sqrt{2}}{2}$,即b2=31a2,
∴c2=b2+a2=32a2,
∴双曲线的离心率为e2=32,
∴双曲线的离心率为e=4$\sqrt{2}$.
故答案为:4$\sqrt{2}$.
点评 本题主要考查了双曲线的简单性质.解题的关键是利用圆中弦长的一半、半径和圆心到直线的距离构成直角三角形,求得圆心到渐近线的距离.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.如图所示,程序框图的输出值S=( )


| A. | 21 | B. | -21 | C. | 15 | D. | 28 |
7.已知x>0,y>0,ln3x+ln9y=ln3,则$\frac{2}{x}+\frac{1}{y}$的最小值是( )
| A. | 6 | B. | $6+\sqrt{2}$ | C. | 8 | D. | $4+2\sqrt{2}$ |
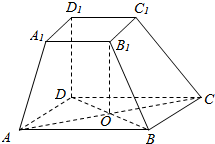 在四棱台ABCD-A1B1C1D1中,D1D⊥ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,∠BAD=60°.
在四棱台ABCD-A1B1C1D1中,D1D⊥ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,∠BAD=60°.