题目内容
2.用一个平面去截一个几何体,得到的截面不可能是圆的几何体是( )| A. | 圆锥 | B. | 圆柱 | C. | 球 | D. | 三棱锥 |
分析 在A中,圆锥的横截面是圆;在B中,圆柱的横截面是圆;在C中,球的横截面是圆;在D中,三棱锥的截面不可能是圆.
解答 解:在A中,圆锥的横截面是圆,故A不成立;
在B中,圆柱的横截面是圆,故B不成立;
在C中,球的横截面是圆,故C不成立;
在D中,三棱锥的截面不可能是圆,故D成立.
故选:D.
点评 本题考查圆锥、圆柱、球、三棱锥的截面图形的判断,是基础题,解题时要认真审题,注意圆锥、圆柱、球、三棱锥的性质的合理运用.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
13.若随机变量X~B(4,$\frac{1}{2}$),则D(2X+1)=( )
| A. | 2 | B. | 4 | C. | 8 | D. | 9 |
10.设m,n是两条不同的直线,α,β是两个不同的平面,且m?α,n?β,下列命题中正确的是( )
| A. | 若α⊥β,则m⊥n | B. | 若α∥β,则m∥n | C. | 若m⊥n,则α⊥β | D. | 若n⊥α,则α⊥β |
14.已知函数f(x)=$\frac{e(x-1)}{{e}^{x}}$,若存在两对关于y轴对称的点分别再直线y=k(x+1)(k≠0)和函数y=f(x)的图象上,则实数k的取值范围是( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (0,1)∪(1,+∞) | D. | (-∞,-1)∪(-1,0) |
12.能推出{an}是递增数列的是( )
| A. | {an}是等差数列且$\left\{{\frac{a_n}{n}}\right\}$递增 | |
| B. | Sn是等差数列{an}的前n项和,且$\left\{{\frac{S_n}{n}}\right\}$递增 | |
| C. | {an}是等比数列,公比为q>1 | |
| D. | 等比数列{an},公比为0<q<1 |
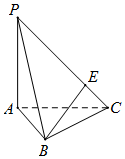 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC,PA=AC,E为PC上的动点,当 BE⊥PC时,$\frac{CE}{PC}$的值为$\frac{1}{4}$.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC,PA=AC,E为PC上的动点,当 BE⊥PC时,$\frac{CE}{PC}$的值为$\frac{1}{4}$.