题目内容
求函数y=log
x+log
(3-x)在0<x<3范围内的最大值和最小值.
| 1 |
| 3 |
| 1 |
| 3 |
考点:对数的运算性质
专题:函数的性质及应用
分析:利用对数运算法则得到y=log
[-(x-
)2+
],由此能求出函数y=log
x+log
(3-x)在0<x<3范围内的最大值和最小值.
| 1 |
| 3 |
| 3 |
| 2 |
| 9 |
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
解答:
解:y=log
x+log
(3-x)
=log
x(3-x)
=log
(3x-x2)
=log
[-(x-
)2+
],
∵0<x<3,
∴0<-(x-
)2+
≤
,
∴y=log
[-(x-
)2+
]≥log
.
∴函数y=log
x+log
(3-x)在0<x<3范围内无最大值,
最小值是log
.
| 1 |
| 3 |
| 1 |
| 3 |
=log
| 1 |
| 3 |
=log
| 1 |
| 3 |
=log
| 1 |
| 3 |
| 3 |
| 2 |
| 9 |
| 4 |
∵0<x<3,
∴0<-(x-
| 3 |
| 2 |
| 9 |
| 4 |
| 9 |
| 4 |
∴y=log
| 1 |
| 3 |
| 3 |
| 2 |
| 9 |
| 4 |
| 1 |
| 3 |
| 9 |
| 4 |
∴函数y=log
| 1 |
| 3 |
| 1 |
| 3 |
最小值是log
| 1 |
| 3 |
| 9 |
| 4 |
点评:本题考查函数的最大值与最小值的求法,是中档题,解题时要注意对数运算法则和配方法的合理运用.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
某几何体三视图如图所示,则该几何几的体积等于( )


| A、2 | B、4 | C、8 | D、12 |
圆台的上下底面半径和高的比为1:4:4,若母线长为10,则圆台的表面积为( )
| A、81π | B、100π |
| C、168π | D、169π |
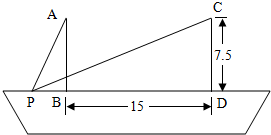 船上两根高7.5m的桅杆相距15m,一条30m长的绳子两端系在桅杆的顶上,并按如图所示的方式绷紧.假设绳子位于两根桅杆所在的平面内,求绳子与甲板接触点P到桅杆AB的距离.
船上两根高7.5m的桅杆相距15m,一条30m长的绳子两端系在桅杆的顶上,并按如图所示的方式绷紧.假设绳子位于两根桅杆所在的平面内,求绳子与甲板接触点P到桅杆AB的距离.