题目内容
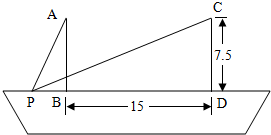船上两根高7.5m的桅杆相距15m，一条30m长的绳子两端系在桅杆的顶上，并按如图所示的方式绷紧．假设绳子位于两根桅杆所在的平面内，求绳子与甲板接触点P到桅杆AB的距离．考点：解三角形的实际应用
专题：应用题,圆锥曲线的定义、性质与方程
分析：由题意，设AC为焦点，则P运动轨迹为椭圆
+
=1（a＞b＞0），求出椭圆方程，即可求出绳子与甲板接触点P到桅杆AB的距离．
| x2 |
| a2 |
| y2 |
| b2 |
解答：
解：由题意，设AC为焦点，则P运动轨迹为椭圆
+
=1（a＞b＞0）
∴2c=|AC|=15，2a=|PA|+|PC|=30
∴b2=a2-c2=
∴椭圆方程为：
+
=1
当y=7.5时，x2=150，解得x=±5
P到AB距离PB=5
-7.5≈4.75m．
| x2 |
| a2 |
| y2 |
| b2 |
∴2c=|AC|=15，2a=|PA|+|PC|=30
∴b2=a2-c2=
| 675 |
| 4 |
∴椭圆方程为：
| x2 |
| 225 |
| y2 | ||
|
当y=7.5时，x2=150，解得x=±5
| 6 |
P到AB距离PB=5
| 6 |
点评：本题考查椭圆的定义，考查椭圆的方程，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
全能测控一本好卷系列答案
相关题目
函数y=2sin2x图象的一条对称轴方程可以为（ ）
A、x=
| ||
B、x=
| ||
C、x=
| ||
| D、x=π |