题目内容
2.已知函数f(x)=x3+2x,若f(1)+f(log${\;}_{\frac{1}{a}}$3)>0(a>0且a≠1),则实数a的取值范围是(0,1)∪(3,+∞).分析 可判断函数f(x)=x3+2x是奇函数,且在R上是增函数,从而化简f(1)+f(log${\;}_{\frac{1}{a}}$3)>0为log${\;}_{\frac{1}{a}}$3>-1;从而解得.
解答 解:∵函数f(x)=x3+2x是奇函数,且在R上是增函数,
∵f(1)+f(log${\;}_{\frac{1}{a}}$3)>0,
∴f(log${\;}_{\frac{1}{a}}$3)>-f(1)=f(-1),
∴log${\;}_{\frac{1}{a}}$3>-1;
∴$\frac{1}{a}$>1或3<a;
即a∈(0,1)∪(3,+∞);
故答案为:(0,1)∪(3,+∞).
点评 本题考查了函数的性质与不等式的解法与应用,属于中档题.

练习册系列答案
相关题目
12.已知全集U=R,集合P={x|x2-2x≤0},Q={y|y=x2-2x},则P∩Q为( )
| A. | [-1,2] | B. | [0,2] | C. | [0,+∞) | D. | [-1,+∞) |
10.已知条件p:x≥1,条件q:$\frac{1}{x}$<1,则¬p是q的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
7.函数f(x)为奇函数,则函数$\frac{{3}^{x}-1}{{3}^{x}+1}$•f(x)为( )
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 既是偶函数,也是奇函数 | D. | 既非偶函数,也非奇函数 |
14.如果ξ是1个离散型随机变量,那么下列命题中假命题是( )
| A. | ξ取每个可能值的概率是非负数 | |
| B. | ξ取所有可能值的概率之和为1 | |
| C. | ξ取某2个可能值的概率等于分别取其中这2个值的概率之和 | |
| D. | ξ的取值只能是正整数 |
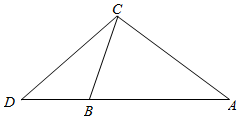 如图,在锐角三角形ABC中,∠A=$\frac{π}{4}$,AC=$\sqrt{3}$,BC=$\sqrt{2}$,BD=$\frac{3\sqrt{2}}{5}$;
如图,在锐角三角形ABC中,∠A=$\frac{π}{4}$,AC=$\sqrt{3}$,BC=$\sqrt{2}$,BD=$\frac{3\sqrt{2}}{5}$;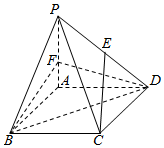 如图,四棱锥P-ABCD中,底面ABCD是边长为3的菱形,∠ABC=60°,PA⊥面ABCD,且PA=3.E为PD中点,F在棱PA上,且AF=1
如图,四棱锥P-ABCD中,底面ABCD是边长为3的菱形,∠ABC=60°,PA⊥面ABCD,且PA=3.E为PD中点,F在棱PA上,且AF=1