题目内容
14.如果ξ是1个离散型随机变量,那么下列命题中假命题是( )| A. | ξ取每个可能值的概率是非负数 | |
| B. | ξ取所有可能值的概率之和为1 | |
| C. | ξ取某2个可能值的概率等于分别取其中这2个值的概率之和 | |
| D. | ξ的取值只能是正整数 |
分析 根据离散型随机变量的分布列的性质,每一个变量对应的概率都非负,所有变量对应的概率之和是1,每一个变量对应的事件是互斥事件,得到结论.
解答 解:根据离散型随机变量的分布列的性质,
A.ξ取每个可能值的概率是非负数,正确,
B.ξ取所有可能值的概率之和为1,正确,
C.每一个变量对应的事件是互斥事件,ξ取某两个可能值的概率等于分别取其中每个值的概率之和,正确,
D.ξ的取值只能是正整数,错误,
故选D.
点评 本题主要考查命题的真假判断,涉及查概率的意义,考查离散型随机变量的分布列的性质,本题是一个概念辨析问题,不需要运算,比较基础..

练习册系列答案
相关题目
4.已知集合A={y|y=2x-1,x∈R},B={x|y=lg(x-2)},则下列结论正确的是( )
| A. | -1∈A | B. | 3∉B | C. | A∪B=B | D. | A∩B=B |
9.把二项式($\frac{x}{2}$-$\frac{1}{\root{3}{x}}$)8的展开式的各项重新排列,则第一项为有理数,且有理项互不相邻的概率为( )
| A. | $\frac{4}{27}$ | B. | $\frac{3}{25}$ | C. | $\frac{5}{28}$ | D. | $\frac{2}{15}$ |
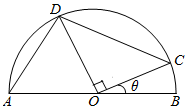 如图,在半径r=8的半圆中,O是圆心,AB是直径,C、D在半圆上滑动,且CO⊥OD.
如图,在半径r=8的半圆中,O是圆心,AB是直径,C、D在半圆上滑动,且CO⊥OD.