题目内容
6.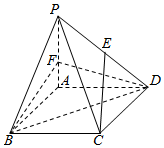 如图,四棱锥P-ABCD中,底面ABCD是边长为3的菱形,∠ABC=60°,PA⊥面ABCD,且PA=3.E为PD中点,F在棱PA上,且AF=1
如图,四棱锥P-ABCD中,底面ABCD是边长为3的菱形,∠ABC=60°,PA⊥面ABCD,且PA=3.E为PD中点,F在棱PA上,且AF=1(Ⅰ)求证:CE∥面BDF;
(Ⅱ)求三棱锥P-BDF的体积.
分析 (Ⅰ)取PF中点G,连接EG,CG.连接AC交BD于O,连接FO.由三角形中位线定理可得FO∥GC,GE∥FD.然后利用平面与平面平行的判定得到面GEC∥面FOD,进一步得到CE∥面BDF;
(Ⅱ)由PA是三棱锥P-ABD的高,求出底面三角形ABD的面积,由三棱锥P-BDF的体积等于三棱锥P-ABD的体积与三棱锥F-ABD的体积差求解.
解答  证明:(Ⅰ)如图所示,取PF中点G,连接EG,CG.
证明:(Ⅰ)如图所示,取PF中点G,连接EG,CG.
连接AC交BD于O,连接FO.
由题可得F为AG中点,O为AC中点,
∴FO∥GC;
又G为PF中点,E为PD中点,
∴GE∥FD.
又GE∩GC=G,GE、GC?面GEC,
FO∩FD=F,FO,FD?面FOD.
∴面GEC∥面FOD.
∵CE?面GEC,
∴CE∥面BDF;
解:(Ⅱ)∵PA⊥面ABCD,
∴PA是三棱锥P-ABD的高,
又${S}_{△ABD}=\frac{1}{2}×3×3×\frac{\sqrt{3}}{2}=\frac{9\sqrt{3}}{4}$,
∴${V}_{P-ABD}=\frac{1}{3}×{S}_{△ABD}×PA=\frac{9\sqrt{3}}{4}$,
同理${V}_{F-ABD}=\frac{1}{3}×{S}_{△ABD}×FA=\frac{3\sqrt{3}}{4}$.
∴${V}_{P-BDF}={V}_{P-ABD}-{V}_{F-ABD}=\frac{3\sqrt{3}}{2}$.
点评 本题考查直线与平面平行的判定,考查了棱锥体积得求法,考查空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
1.下列命题中错误的是( )
| A. | 圆柱的轴截面是过母线的截面中面积最大的一个 | |
| B. | 圆锥的轴截面是所在过顶点的截面中面积最大的一个 | |
| C. | 圆台的所有平行于底面的截面都是圆面 | |
| D. | 圆锥所有的轴截面是全等的等腰三角形 |
11.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为e,一条渐近线的方程为y=$\sqrt{2e-1}$x,则e=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$ |