Question

11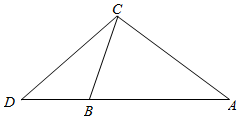．如图，在锐角三角形ABC中，∠A=$\frac{π}{4}$，AC=$\sqrt{3}$，BC=$\sqrt{2}$，BD=$\frac{3\sqrt{2}}{5}$；
（1）求∠ABC；
（2）求CD的长度；
（3）求sinD．

Answer 1

分析 （1）由题意和正弦定理可得sin∠ABC=$\frac{ACsinA}{BC}$，代值计算可得；
（2）由（1）可得∠CBD=120°，在△BCD中由余弦定理可得；
（3）由正弦定理可得sinD=$\frac{BCsin∠CBD}{CD}$，代值计算可得．

解答 解：（1）由题意和正弦定理可得：
sin∠ABC=$\frac{ACsinA}{BC}$=$\frac{\sqrt{3}×\frac{\sqrt{2}}{2}}{\sqrt{2}}$=$\frac{\sqrt{3}}{2}$，
在锐角三角形ABC中，∠ABC=60°；
（2）由（1）可得∠CBD=180°-∠ABC=120°，
∴在△BCD中由余弦定理可得CD²=BC²+BD²-2BC•BD•cos∠CBD
=2+$\frac{18}{25}$-2×$\sqrt{2}$×$\frac{3\sqrt{2}}{5}$×（-$\frac{1}{2}$）=$\frac{98}{25}$，故CD=$\frac{7\sqrt{2}}{5}$；
（3）由正弦定理可得sinD=$\frac{BCsin∠CBD}{CD}$=$\frac{\sqrt{2}×\frac{\sqrt{3}}{2}}{\frac{7\sqrt{2}}{5}}$=$\frac{5\sqrt{3}}{14}$

点评 本题考查正弦定理解三角形，涉及余弦定理求边的长度，属基础题．