题目内容
13.在等差数列{an}中,Sn为数列{an}的前n项和,d为数列{an}的公差,若对任意n∈N*,都有Sn>0,且a2a4=9,则d的取值范围为$[0,\sqrt{3})$.分析 对任意n∈N*,都有Sn>0,可得:a1>0,d≥0.由于a2a4=9,化为3d2+4a1d+${a}_{1}^{2}$-9=0,△>0,而且两根之和=-4d<0,而必须至少有一个正实数根.可得3d2-9≤0,d≥0,解出即可得出.
解答 解:对任意n∈N*,都有Sn>0,∴a1>0,d≥0.
∵a2a4=9,
∴(a1+d)(a1+3d)=9,
化为${a}_{1}^{2}$+4a1d+3d2-9=0,
△=16d2-4(3d2-9)=4d2+36>0,
∴方程有两个不相等的实数根,
并且两根之和为-4d<0,而必须至少有一个正实数根.
d=$\sqrt{3}$时,a1=0,舍去.
则d的取值范围为$[0,\sqrt{3})$.
故答案为:$[0,\sqrt{3})$.
点评 本题考查了等差数列的通项公式及其前n项和公式、一元二次方程的实数根与判别式的关系、一元二次不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知集合A={y|y=2x-1,x∈R},B={x|y=lg(x-2)},则下列结论正确的是( )
| A. | -1∈A | B. | 3∉B | C. | A∪B=B | D. | A∩B=B |
1.已知集合A={(x,y)|-1≤x≤2且0≤y≤4},集合B={(x,y)|0≤y≤x2},在A中任取一点P,则P∈B的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
8.执行如图的程序框图,若输入n值为4,则输出的结果为( )


| A. | 8 | B. | 21 | C. | 34 | D. | 55 |
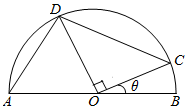 如图,在半径r=8的半圆中,O是圆心,AB是直径,C、D在半圆上滑动,且CO⊥OD.
如图,在半径r=8的半圆中,O是圆心,AB是直径,C、D在半圆上滑动,且CO⊥OD.