题目内容
函数f(x)=
的最大值与最小值之积等于 .
| x+x3 |
| x4+2x2+1 |
考点:函数的最值及其几何意义
专题:计算题,不等式的解法及应用
分析:分类讨论,利用基本不等式,求出函数f(x)=
的最大值与最小值,即可得出结论.
| x+x3 |
| x4+2x2+1 |
解答:
解:f(x)=
=
,
x=0时,f(0)=0,
x≠0时,f(x)=
,
x>0时,x+
≥2,
∴0<f(x)≤
,
x<0时,x+
≤-2,
∴-
≤f(x)<0,
综上,∴-
≤f(x)≤
,
∴函数f(x)=
的最大值与最小值之积等于-
.
故答案为:-
.
| x+x3 |
| x4+2x2+1 |
| x |
| 1+x2 |
x=0时,f(0)=0,
x≠0时,f(x)=
| 1 | ||
x+
|
x>0时,x+
| 1 |
| x |
∴0<f(x)≤
| 1 |
| 2 |
x<0时,x+
| 1 |
| x |
∴-
| 1 |
| 2 |
综上,∴-
| 1 |
| 2 |
| 1 |
| 2 |
∴函数f(x)=
| x+x3 |
| x4+2x2+1 |
| 1 |
| 4 |
故答案为:-
| 1 |
| 4 |
点评:本题考查函数的最值及其几何意义,考查基本不等式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
函数f(x)=-sinx+1的图象大致为( )
A、 |
B、 |
C、 |
D、 |
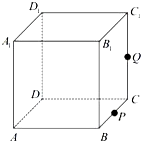 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是