Question

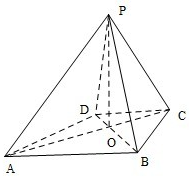如图，已知四棱锥P-ABCD的底面ABCD为等腰梯形，AB∥DC，AC⊥BD，AC与BD相交于点O，且顶点P在底面上的射影恰为O点，又BO=2，PO=

2

，PB⊥PD．
（1）求异面直接PD与BC所成角的余弦值；
（2）求二面角P-AB-C的大小；
（3）设点M在棱PC上，且

PM

PC

=λ，问λ为何值时，PC⊥平面BMD．

Answer 1

考点：二面角的平面角及求法,异面直线及其所成的角

专题：空间位置关系与距离

分析：（1）由已知得到PO⊥平面ABCD，利用线面垂直的性质得到PO⊥BD，过D做DE∥BC交于AB于E，连接PE，则∠PDE或其补角为异面直线PD与BC所成的角，利用平面几何的知识解答；
（2）连接OE，由（1）以及三垂线定理可知，∠PEO为二面角P-AB-C的平面角，然后求值；
（3）连接MD，MB，MO，利用PC⊥平面BMD，得到PC⊥OM，Rt△POC中求的PM=

2 3

3

，MC=

3

3

．

解答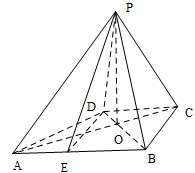： 解：（1）∵PO⊥平面ABCD，∴PO⊥BD
又PB⊥PD，BO=2，PO=

2

，
由平面几何知识得：OD=1，PD=

3

，PB=

6

过D做DE∥BC交于AB于E，连接PE，则∠PDE或其补角为异面直线PD与BC所成的角，
∵四边形ABCD是等腰梯形，
∴OC=OD=1，OB=OA=2，OA⊥OB
∴BC=

5

，AB=2

2

，CD=

2

又AB∥DC
∴四边形EBCD是平行四边形．
∴ED=BC=

5

，BE=CD=

2

∴E是AB的中点，且AE=

2

又PA=PB=

6

，
∴△PEA为直角三角形，
∴PE=

PA2-AE2

=

6-2

=2
在△PED中，由余弦定理得cos∠PDE=

PD2+DE2-PE2

2PD•DE

=

3+5-4

2• 3 • 5

=

2 15

15

故异面直线PD与BC所成的角的余弦值为

2 15

15

；
（2）连接OE，由（1）以及三垂线定理可知，∠PEO为二面角P-AB-C的平面角，
∴sin∠PE0=

PO

PE

=

2

2

，∴∠PEO=45°，∴二面角P-AB-C的平面角的大小为45°；
（3）连接MD，MB，MO，
∵PC⊥平面BMD，OM?平面BMD，
∴PC⊥OM，
在Rt△POC中，PC=PD=

3

，OC=1，PO=

2

，
∴PM=

2 3

3

，MC=

3

3

，
∴

PM

MC

=2，
故λ=2时，PC⊥平面BMD．

点评：本题考查了异面直线所成的角及二面角的平面角的求法；关键是将空间角转化为平面角解答．