题目内容
已知函数f(x)=2x-
,且2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,则实数m的取值范围是 .
| 1 |
| 2x |
考点:函数恒成立问题
专题:函数的性质及应用
分析:先将已知代入,然后进行化简(用到因式分解),然后将问题转化为函数的最值问题求解.
解答:
解:由f(x)=2x-
得2tf(2t)+mf(t)≥0,
即2t(22t-
)+m(2t-
)≥0当t∈[1,2]时恒成立.
即2t(2t+
)(2t-
)+m(2t-
)≥0①在[1,2]上恒成立;
因为当t在区间[1,2]上取值时,2t>1,所以2t-
>0.
所以①式可化为(2t)2+m+1≥0恒成立,显然当t=1时(2t)2+m+1取最小值,即5+m≥0,所以m≥-5.
故答案为m≥-5.
| 1 |
| 2x |
即2t(22t-
| 1 |
| 22t |
| 1 |
| 2t |
即2t(2t+
| 1 |
| 2t |
| 1 |
| 2t |
| 1 |
| 2t |
因为当t在区间[1,2]上取值时,2t>1,所以2t-
| 1 |
| 2t |
所以①式可化为(2t)2+m+1≥0恒成立,显然当t=1时(2t)2+m+1取最小值,即5+m≥0,所以m≥-5.
故答案为m≥-5.
点评:本题考查了不等式的恒成立问题,一般转化为函数的最值问题求解.

练习册系列答案
相关题目
已知函数f(x)=
,若存在x1,x2,当0≤x1<4≤x2≤6时,f(x1)=f(x2),则x1•f(x2)的取值范围是( )
|
| A、[0,1) |
| B、[1,4] |
| C、[1,6] |
| D、[0,1]∪[3,8] |
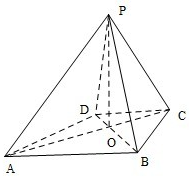 如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=
如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=