题目内容
已知函数f(x)=cos(x-
)-mcosx+
是奇函数.
(1)求函数f(x)的最小正周期以及对称轴方程;
(2)△ABC内角A、B、C的对边分别为a、b、c,若f(B)=
,b=1,c=
,且a>b,试判断△ABC的形状,并说明理由.
| 2π |
| 3 |
| 3 |
| 2 |
(1)求函数f(x)的最小正周期以及对称轴方程;
(2)△ABC内角A、B、C的对边分别为a、b、c,若f(B)=
3-
| ||
| 2 |
| 3 |
考点:余弦定理,两角和与差的余弦函数,三角函数的周期性及其求法
专题:三角函数的图像与性质,解三角形
分析:(1)先求得m的值,即可化简求得函数f(x)的解析式,从而可求最小正周期以及对称轴方程;
(2)由已知,可先求得B,由余弦定理可得a=b=1,从而可判断△ABC的形状为等腰三角形.
(2)由已知,可先求得B,由余弦定理可得a=b=1,从而可判断△ABC的形状为等腰三角形.
解答:
解:(1)函数f(x)=cos(x-
)-mcosx+
是奇函数.
∴f(0)=0
即cos
-m+
=0
解得m=1
∴f(x)=-
cosx+
sinx-cosx+
=-
cosx+
sinx+
=
sin(x-
)+
∴T=
=2π,对称轴x=kπ+
,k∈Z
(2)∵f(B)=-
cosB+
sinB+
=
∴
cosB-sinB=1
∴2cos(B+
)=1
∴B+
=
∴B=
又∵b=1,c=
∴cosB=
解得a=1
∴△ABC为等腰三角形.
| 2π |
| 3 |
| 3 |
| 2 |
∴f(0)=0
即cos
| 2π |
| 3 |
| 3 |
| 2 |
解得m=1
∴f(x)=-
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
=-
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
=
| 3 |
| π |
| 3 |
| 3 |
| 2 |
∴T=
| 2π |
| 1 |
| 5π |
| 6 |
(2)∵f(B)=-
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
3-
| ||
| 2 |
∴
| 3 |
∴2cos(B+
| π |
| 6 |
∴B+
| π |
| 6 |
| π |
| 3 |
∴B=
| π |
| 6 |
又∵b=1,c=
| 3 |
∴cosB=
| a2+c2-b2 |
| 2ac |
解得a=1
∴△ABC为等腰三角形.
点评:本题主要考察了两角和与差的余弦函数,余弦定理的应用,三角函数的周期性及其求法,属于中档题.

练习册系列答案
相关题目
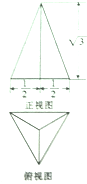
已知三棱锥的底面是正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
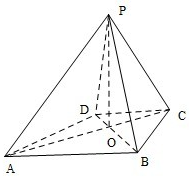 如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=
如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=