题目内容
已知a为第三象限角,f(α)=
.
(1)化简f(α);
(2)若cos(α-π)=
,求f(α)的值.
sin(α-
| ||
| tan(-α-2π)sin(-α-π) |
(1)化简f(α);
(2)若cos(α-π)=
| 1 |
| 5 |
考点:运用诱导公式化简求值,同角三角函数基本关系的运用
专题:计算题,三角函数的求值
分析:(1)运用诱导公式即可化简.
(2)由已知可求得cosα,由α为第三象限角,可求sinα的值,代入f(α)=
即可求值.
(2)由已知可求得cosα,由α为第三象限角,可求sinα的值,代入f(α)=
| cos2α |
| sinα |
解答:
解:(1)f(α)=
=
=
.
(2)∵cos(α-π)=
,
∴可得:cosα=-
,
∵α为第三象限角,
∴sinα=-
=-
,
∴f(α)=
=
=-
.
sin(a-
| ||
| tan(-α-2π)sin(-α-π) |
| (-cosα)(-cosα)(-tanα) |
| (-tanα)sinα |
| cos2α |
| sinα |
(2)∵cos(α-π)=
| 1 |
| 5 |
∴可得:cosα=-
| 1 |
| 5 |
∵α为第三象限角,
∴sinα=-
| 1-cos2α |
2
| ||
| 5 |
∴f(α)=
| cos2α |
| sinα |
| ||||
-
|
| ||
| 60 |
点评:本题主要考查了运用诱导公式化简求值,考查了同角三角函数基本关系的运用,属于基础题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
已知命题p:“?a”的否定是“?x0<0,x02+x0-1≥0”;命题q:在△ABC中“∠A>∠B”的充要条件是“sinA>sinB”;则下列命题是假命题的是( )
| A、p∨q |
| B、p∨(?q) |
| C、(?p)∨q |
| D、(?p)∨(?q) |
设f(x)=
,则f(1)的值为( )
|
| A、0 | B、1 | C、2 | D、-1 |
已知集合M={0,1,2},N={x},若M∪N={0,1,2,3},则x的值为( )
| A、3 | B、2 | C、1 | D、0 |
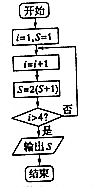 在如图所示的程序框图表示的算法中,输出的结果是
在如图所示的程序框图表示的算法中,输出的结果是 已知,如图,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E.
已知,如图,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E.