题目内容
4.已知f(x)=(x-a)(x-3a)(其中a>0),g(x)=x2+1;条件p:实数x满足f(x)<0;条件q:实数x满足4<g′(x)≤6.(1)若a=1,且“p∧q”为真,求实数x的取值范围;
(2)若q是p的充分不必要条件,求实数a的取值范围.
分析 (1)若a=1,求出命题p,q的等价条件,利用p∧q为真,则p,q为真,即可求实数x的取值范围;
(2)求出命题p,q的等价条件,利用q是p的充分不必要条件,即可求实数a的取值范围.
解答 解:(1)若a=1,不等式为(x-a)(x-3a)<0为(x-1)(x-3)<0,
即1<x<3,即p:1<x<3,
由4<g′(x)≤6.
得4<2x≤6.
则2<x≤3,即q:2<x≤3,
若p∧q为真,则p,q同时为真,
即$\left\{\begin{array}{l}{1<x<3}\\{2<x≤3}\end{array}\right.$得1<x<3,
即实数x的取值范围是1<x<3.
(2)由f(x)=(x-a)(x-3a)<0得a<x<3a,即p:a<x<3a
若q是p的充分不必要条件,则q⇒p且p⇒q不成立,
即$\left\{\begin{array}{l}{a≤2}\\{3a>3}\end{array}\right.$,即1<a≤2,
所以实数a的取值范围是1<a≤2.
点评 本题主要考查充分条件和必要条件的应用,以及不等式的求解,利用不等式的解法时解决本题的关键.

练习册系列答案
相关题目
15.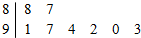 某市8所中学生参加比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
某市8所中学生参加比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
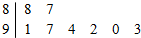 某市8所中学生参加比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
某市8所中学生参加比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91 5.5 | B. | 91 5 | C. | 92 5.5 | D. | 92 5 |
12.使得函数f(x)=log2x+x-5有零点的一个区间是( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
9.已知直线y=kx-1与直线x+2y+3=0垂直,则k的是( )
| A. | 3 | B. | 1 | C. | -1 | D. | 2 |
16.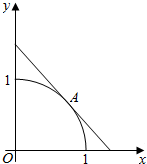 如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上中点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的值为( )
如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上中点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的值为( )
 如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上中点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的值为( )
如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上中点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的值为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
13.已知扇形的中心角为$\frac{π}{3}$,半径为2,则其面积为( )
| A. | $\frac{π}{6}$ | B. | $\frac{4π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |