题目内容
9．已知直线y=kx-1与直线x+2y+3=0垂直，则k的是（ ）| A． | 3 | B． | 1 | C． | -1 | D． | 2 |
分析 根据两条直线垂直，它们的斜率之积等于-1，求出k的值．
解答 解：∵直线y=kx-1与直线x+2y+3=0垂直，
∴k=2；
故选：D．
点评 本题考查了两条直线垂直的判定与应用问题，解题时应用两直线垂直，斜率之积等于-1，即可得出答案．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
19．为考察某种药物预防禽流感的效果，进行动物家禽试验，调查了100个样本，统计结果为：服用药的共有60个样本，服用药但患病的仍有20个样本，没有服用药且未患病的有20个样本．
（1）根据所给样本数据完成下面2×2列联表；
（2）请问能否有90%把握认为药物有效？
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．
（1）根据所给样本数据完成下面2×2列联表；
（2）请问能否有90%把握认为药物有效？
| 不得禽流感 | 得禽流感 | 总 计 | |
| 服 药 | 40 | 20 | 60 |
| 不服药 | 20 | 20 | 40 |
| 总 计 | 60 | 40 | 100 |
| P（K2≥k） | 0.10 | 0.05 | 0.010 | 0.001 |
| k | 2.072 | 3.841 | 6.635 | 10.828 |
20．
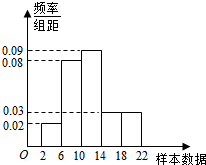样本容量为100的频率分布直方图如图所示．根据样本的频率分布直方图估计样本数据落在[6，10）内的频数为a，样本数据落在[2，10）内的频率为b，则a，b分别是（ ）
样本容量为100的频率分布直方图如图所示．根据样本的频率分布直方图估计样本数据落在[6，10）内的频数为a，样本数据落在[2，10）内的频率为b，则a，b分别是（ ）| A． | 32，0.4 | B． | 8，0.1 | C． | 32，0.1 | D． | 8，0.4 |
18．命题“?x0∈R，x0+1＜0或${x_0}^2-{x_0}＞0$”的否定形式是（ ）
| A． | ?x0∈R，x0+1≥0或${x_0}^2-{x_0}≤0$ | B． | ?x0∈R，x0+1≥0或${x_0}^2-{x_0}≤0$ | ||
| C． | ?x0∈R，x0+1≥0且${x_0}^2-{x_0}≤0$ | D． | ?x0∈R，x0+1≥0且${x_0}^2-{x_0}≤0$ |