题目内容
四人赛跑,假设其跑过的路程和时间的函数关系分别是f1(x)=x2,f2(x)=4x,f3(x)=log2x,f4(x)=2x如果他们一直跑下去,最终跑在最前面的人具有的函数关系是 .
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:根据题意,本题实际考查各类函数的增长模型,通过对四类函数分析,指数函数增长最快,选出选项.
解答:
解:根据题意,最终跑在最前面的人一为函数值最大的函数,
通过分析各种类型函数的增长f1(x)=x2,f2(x)=4x,f3(x)=log2x,f4(x)=2x中,f4(x)=2x增长最快,如图
故答案为:f4(x)=2x.
通过分析各种类型函数的增长f1(x)=x2,f2(x)=4x,f3(x)=log2x,f4(x)=2x中,f4(x)=2x增长最快,如图

故答案为:f4(x)=2x.
点评:本题考查根据实际问题选择函数类型,通过对二次函数,一次函数,对数函数,指数函数的分析选出选项,属于基础题.

练习册系列答案
相关题目
不等式2x+3-x2>0的解集是( )
| A、{x|-1<x<3} |
| B、{x|x>3或x<-1} |
| C、{x|-3<x<1} |
| D、{x|x>1或x<-3} |
已知焦点在y轴上的椭圆
+
=1的长轴长为8,则m等于( )
| x2 |
| 10 |
| y2 |
| m |
| A、4 | B、8 | C、10 | D、16 |
已知直线y=k(x+1)与抛物线C:y2=4x相交于A、B两点,F为抛物线C的焦点,若|FA|=2|FB|,则k=( )
A、±
| ||||
B、±
| ||||
C、±
| ||||
D、
|
如图,正六边形ABCDEF中,
+
+
=( )
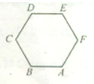
| BA |
| CD |
| BC |

A、
| ||
B、
| ||
C、
| ||
D、
|
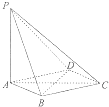 如图,在四棱锥P-ABCD中,PA丄平面ABCD,底面ABCD是菱形AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA丄平面ABCD,底面ABCD是菱形AB=2,∠BAD=60°. 据气象中心观察和预测:发生于M第的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为时间t(h)内沙尘暴所经过的路程s(km)
据气象中心观察和预测:发生于M第的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为时间t(h)内沙尘暴所经过的路程s(km)