题目内容
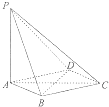 如图,在四棱锥P-ABCD中,PA丄平面ABCD,底面ABCD是菱形AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA丄平面ABCD,底面ABCD是菱形AB=2,∠BAD=60°.(Ⅰ)求证:BD丄平面PAC;
(Ⅱ)若PA=Ab,求四棱锥P-ABCD的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)根据菱形得出AC⊥BD,再运用判定定理可证明,(Ⅱ)求出高线PA=2,运用四棱锥P-ABCD的体积公式求解.
解答:
证明:(Ⅰ)∵底面ABCD是菱形,
∴AC⊥BD,
∵PA丄平面ABCD,
∴PA丄BD
∴BD丄平面PAC;
解:(Ⅱ)∵PA=AB,
∴PA=2,
∵底面ABCD是菱形AB=2,∠BAD=60°.
∴S平行四边形ABCD=2
,
∴四棱锥P-ABCD的体积=
×2
×2=
∴AC⊥BD,
∵PA丄平面ABCD,
∴PA丄BD
∴BD丄平面PAC;
解:(Ⅱ)∵PA=AB,
∴PA=2,
∵底面ABCD是菱形AB=2,∠BAD=60°.
∴S平行四边形ABCD=2
| 3 |
∴四棱锥P-ABCD的体积=
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
点评:本题考查了空间几何体中的线面垂直问题,体积的求解,关键是抓住定理,公式的条件,属于中档题.

练习册系列答案
 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
已知点A(2
,
)在椭圆
+
=1上,则椭圆的离心率为( )
| 6 |
| 3 |
| 5 |
| x2 |
| a2 |
| y2 |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线的渐近线为y=±
x,焦点坐标为(-4,0),(4,0),则双曲线方程为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=
+lg(3x+1)的定义域为( )
| x2+4 | ||
|
A、(-
| ||||
B、(-∞,-
| ||||
C、(-
| ||||
D、(-
|



