题目内容
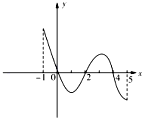 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.| x | -1 | 0 | 2 | 4 | 5 |
| y | 1 | 2 | 0 | 2 | 1 |
| A、[1,2) |
| B、[1,2] |
| C、(2,3) |
| D、[1,3) |
考点:根的存在性及根的个数判断,导数的运算
专题:函数的性质及应用,导数的综合应用
分析:先由导函数的图象和原函数的关系画出原函数的大致图象,再借助与图象分析出函数y=f(x)与直线y=a的图象交点的个数,进而得到函数y=f(x)-a有4个零点时,a的取值范围.
解答:
解:由导函数y=f′(x)的图象可知,函数在[-1,0],[2,4]上为增函数,
则[0,2],[4,5]上为减函数,
且函数在x=0和x=4取得极大值f(0)=2,f(4)=2,
在x=2取得极小值f(2)=0,
则函数f(x)的大致图象如图:
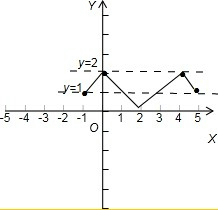
由图得若函数y=f(x)-a有4个零点,
则函数y=f(x)与直线y=a的图象有四个交点
故-1≤a<2
故a的取值范围为[1,2),
故选:A
则[0,2],[4,5]上为减函数,
且函数在x=0和x=4取得极大值f(0)=2,f(4)=2,
在x=2取得极小值f(2)=0,
则函数f(x)的大致图象如图:

由图得若函数y=f(x)-a有4个零点,
则函数y=f(x)与直线y=a的图象有四个交点
故-1≤a<2
故a的取值范围为[1,2),
故选:A
点评:本题主要考查导函数和原函数的单调性之间的关系.利用数形结合是解决本题的关键.

练习册系列答案
相关题目
下列结论正确的是( )
①“a=1”是“直线x-ay=0与直线x+ay=0互相垂直”的充要条件
②函数f(x)=sin(2x-
)最小正周期为π,且图象关于直线x=
对称
③线性回归直线至少经过样本点中的一个
④?x∈R,2x-1≥0的否定是?x∈R,2x-1<0.
①“a=1”是“直线x-ay=0与直线x+ay=0互相垂直”的充要条件
②函数f(x)=sin(2x-
| π |
| 6 |
| π |
| 3 |
③线性回归直线至少经过样本点中的一个
④?x∈R,2x-1≥0的否定是?x∈R,2x-1<0.
| A、② | B、②④ | C、①②③ | D、①②④ |
在(x2-
)5的展开式中,第4项的系数是( )
| 1 |
| x |
| A、∁54 |
| B、-∁54 |
| C、∁53 |
| D、-C53 |
在△ABC中,a=
,b=
,B=
,则A等于( )
| 2 |
| 3 |
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设f(x)=logax(a>0且a≠1),若f(2)=
,则f(
)=( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、2 | ||
| B、-2 | ||
C、-
| ||
D、
|