题目内容
过点P（0，-1）作直线l，若直线l与连接A（1，-2），B（2，1）的线段没有公共点，则直线l的倾斜角的取值范围是 ．
考点：直线的倾斜角
专题：直线与圆
分析：利用斜率计算公式可得kPA=-1，kPB=1．可得直线PA，PB的倾斜角分别为135°，45°．由于直线l与连接A（1，-2），B（2，1）的线段没有公共点，可得直线l的斜率k满足k＞1或k＜-1，即可得出．
解答：
解：∵kPA=
=-1，kPB=
=1．
∴直线PA，PB的倾斜角分别为135°，45°．
∵直线l与连接A（1，-2），B（2，1）的线段没有公共点，
∴直线l的斜率k满足k＞1或k＜-1，
∴直线l的倾斜角的取值范围是（45°，135°）．
故答案为：（45°，135°）．
| -2-(-1) |
| 1-0 |
| -1-1 |
| 0-2 |
∴直线PA，PB的倾斜角分别为135°，45°．
∵直线l与连接A（1，-2），B（2，1）的线段没有公共点，
∴直线l的斜率k满足k＞1或k＜-1，
∴直线l的倾斜角的取值范围是（45°，135°）．
故答案为：（45°，135°）．
点评：本题考查了直线的倾斜角与斜率的关系，考查了计算能力，属于基础题．
练习册系列答案
相关题目
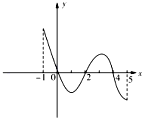已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示．| x | -1 | 0 | 2 | 4 | 5 |
| y | 1 | 2 | 0 | 2 | 1 |
| A、[1，2） |
| B、[1，2] |
| C、（2，3） |
| D、[1，3） |
若书架上有中文书5本，英文书3本，日文书2本，则随机抽取一本恰为外文书的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设tanα、tanβ是方程x2+x-2=0的两实数根，则tan（α+β）的值为（ ）
| A、-1 | ||
B、-
| ||
C、
| ||
| D、1 |
已知α是第二象限角，P（x，
）为其终边上一点，且cosα=
x，则x=（ ）
| 5 |
| ||
| 4 |
A、
| ||
B、±
| ||
C、-
| ||
D、-
|