题目内容
某校从参加高二年级省学业水平模拟考试的学生中抽出50名学生,并统计了他们的数学成绩,成绩的频率分布直方图如图3所示,其中成绩分组区间是:[40,50)[50,60)[60,70)[70,80)[80,90)[90,100].
(Ⅰ)求图中m的值,估计此次考试成绩的众数;
(Ⅱ)为了帮助成绩弱的学生能顺利通过省学业水平考试,学校决定成立“二帮一”学习小组.在样本中从[90,100]分数段的同学中选两位共同帮助[40,50)分数段的同学中的某一位,已知甲同学的成绩为45分,乙同学成绩96分,求甲、乙两同学恰好被安排在同一小组的概率.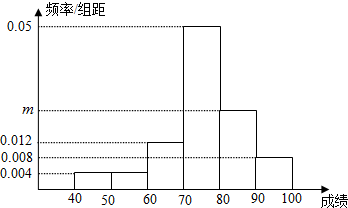
(Ⅰ)求图中m的值,估计此次考试成绩的众数;
(Ⅱ)为了帮助成绩弱的学生能顺利通过省学业水平考试,学校决定成立“二帮一”学习小组.在样本中从[90,100]分数段的同学中选两位共同帮助[40,50)分数段的同学中的某一位,已知甲同学的成绩为45分,乙同学成绩96分,求甲、乙两同学恰好被安排在同一小组的概率.

考点:频率分布直方图,列举法计算基本事件数及事件发生的概率
专题:图表型
分析:(1)根据所有矩形的面积和为1可求出m的值,众数就是分布图里最高的那条,从而可得结论;
(2)先算出成绩在[40,50)分数段内的人数,以及成绩在[90,100]分数段内的人数,列出所有的“二帮一”小组分组办法的基本事件,以及甲、乙两同学被分在同一小组的基本事件,最后利用古典概型的概率公式解之即可.
(2)先算出成绩在[40,50)分数段内的人数,以及成绩在[90,100]分数段内的人数,列出所有的“二帮一”小组分组办法的基本事件,以及甲、乙两同学被分在同一小组的基本事件,最后利用古典概型的概率公式解之即可.
解答:
解:(1)因为所有矩形的面积和为1,所以0.04+0.04+0.12+0.5+10m+0.08=1,
解得m=0.022,
众数就是分布图里最高的那条,即[70,80]的中点横坐标75.
(2)成绩在[40,50)分数段内的人数为50×0.04=2人
成绩在[90,100]分数段内的人数为50×0.08=4人,
[40,50)内有2人,记为甲、A.
[90,100)内有4人,记为乙、B、C、D.
则“二帮一”小组有以下12种分组办法:甲乙B,甲乙C,甲乙D,甲BC,甲BD,甲CD,A乙B,A乙C,A乙D,ABC,ABD,ACD,
其中甲、乙两同学被分在同一小组有3种办法:甲乙B,甲乙C,甲乙D,
所以甲乙两同学恰好被安排在同一小组的概率
=
.
解得m=0.022,
众数就是分布图里最高的那条,即[70,80]的中点横坐标75.
(2)成绩在[40,50)分数段内的人数为50×0.04=2人
成绩在[90,100]分数段内的人数为50×0.08=4人,
[40,50)内有2人,记为甲、A.
[90,100)内有4人,记为乙、B、C、D.
则“二帮一”小组有以下12种分组办法:甲乙B,甲乙C,甲乙D,甲BC,甲BD,甲CD,A乙B,A乙C,A乙D,ABC,ABD,ACD,
其中甲、乙两同学被分在同一小组有3种办法:甲乙B,甲乙C,甲乙D,
所以甲乙两同学恰好被安排在同一小组的概率
| 3 |
| 12 |
| 1 |
| 4 |
点评:本小题主要考查频率、频数、统计和概率等知识,考查数形结合、化归与转化的数学思想方法,以及运算求解能力.

练习册系列答案
相关题目
已知函数f(
)=x+
-2,则f(x)=( )
| 1 |
| x |
| 1 |
| x |
A、x+
| ||
B、=x+
| ||
C、x+
| ||
D、x+
|