题目内容
在直角坐标系中,直线l的参数方程为
(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,已知曲线C的极坐标方程为ρ=2cosθ,若直线l与曲线C相切,则k的值是 .
|
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把曲线C的极坐标方程化为直角坐标方程,可得圆心与半径,利用直线与圆的相切的性质即可得出.
解答:
解:曲线C的极坐标方程为ρ=2cosθ,化为ρ2=2ρcosθ,即x2+y2=2x,化为(x-1)2+y2=1.
可得圆心C(1,0),半径r=1.
由直线l的参数方程
,消去参数t,可得y=kx+1.
∵直线l与曲线C相切,
∴
=1,解得k=0.
故答案为:0.
可得圆心C(1,0),半径r=1.
由直线l的参数方程
|
∵直线l与曲线C相切,
∴
| |k+1| | ||
|
故答案为:0.
点评:本题考查了直线与圆的位置关系、极坐标方程化为直角坐标方程、点到直线的距离公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
若{a2,0,-1}={a,b,0},则a2014+b2014的值为( )
| A、0 | B、1 | C、-1 | D、2 |
下面命题中为假命题的是( )
| A、?x∈R,3x>0 |
| B、?α,β∈R,使sin(α+β)=sinα+sinβ |
| C、“x>2”是“x2-3x+2>0”的充分不必要条件 |
| D、命题“?x∈R,x2+1>3x”的否定是“?x∈R,x2+1<3x” |
在直角坐标系xOy中,直线l经过点P(-1,0),其倾斜角为α,以原点O为极点,以x轴非负半轴为极轴,与直角坐标系xOy取相同的长度单位,建立极坐标系,设曲线C的极坐标方程为ρ2-6ρcosθ+5=0,若直线l与曲线C有公共点,则α的取值范围是( )
A、(0,
| ||||||||
B、[
| ||||||||
C、(
| ||||||||
D、[0,
|
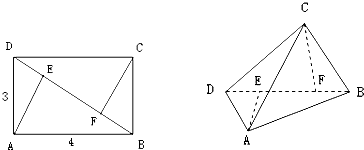 如图,已知矩形ABCD中,AB=2,AD=1,AE⊥BD,CF⊥BD,沿对角线BD把△BCD折起,使二面角C-BD-A的大小为60°,则线段AC的长为
如图,已知矩形ABCD中,AB=2,AD=1,AE⊥BD,CF⊥BD,沿对角线BD把△BCD折起,使二面角C-BD-A的大小为60°,则线段AC的长为 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<