题目内容
设函数f(x)=
(Ⅰ)当a=3时,求函数f(x)的定义域;
(Ⅱ)若函数f(x)的定义域为R,求实数a的取值范围.
| |x-1|+|x+1|-a |
(Ⅰ)当a=3时,求函数f(x)的定义域;
(Ⅱ)若函数f(x)的定义域为R,求实数a的取值范围.
考点:函数的定义域及其求法,函数的值域
专题:不等式
分析:(Ⅰ)a=3时,依题意得出|x-1|+|x+1|≥3;
(法一)由绝对值的几何意义求出不等式的解集,(法二)用分类讨论法求出不等式的解集;
(Ⅱ)依题意得出关于x的不等式|x-1|+|x+1|-a≥0在R上恒成立,化为求|x-1|+|x+1|在R上的最小值即可.
(法一)由绝对值的几何意义求出不等式的解集,(法二)用分类讨论法求出不等式的解集;
(Ⅱ)依题意得出关于x的不等式|x-1|+|x+1|-a≥0在R上恒成立,化为求|x-1|+|x+1|在R上的最小值即可.
解答:
解:(Ⅰ)当a=3时,依题意得:|x-1|+|x+1|≥3;
(法一)由绝对值的几何意义,如图所示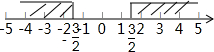 ;
;
∴不等式的解集为{x|x≤-
或x≥
};
(法二)不等式可化为
,或
,或
;
∴不等式的解集为{x|x≤-
或x≥
}.
(Ⅱ)依题意得:关于x的不等式|x-1|+|x+1|-a≥0在R上恒成立,
即a≤|x-1|+|x+1|在R上恒成立;
∵|x-1|+|x+1|≥|(x-1)-(x+1)|=2,
∴a≤2;
∴a的取值范围是{a|a≤2}.
(法一)由绝对值的几何意义,如图所示
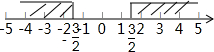 ;
;∴不等式的解集为{x|x≤-
| 3 |
| 2 |
| 3 |
| 2 |
(法二)不等式可化为
|
|
|
∴不等式的解集为{x|x≤-
| 3 |
| 2 |
| 3 |
| 2 |
(Ⅱ)依题意得:关于x的不等式|x-1|+|x+1|-a≥0在R上恒成立,
即a≤|x-1|+|x+1|在R上恒成立;
∵|x-1|+|x+1|≥|(x-1)-(x+1)|=2,
∴a≤2;
∴a的取值范围是{a|a≤2}.
点评:本题考查了不等式的应用问题,解题时应根据题意,得出不等式(组),解不等式(组),从而求出符合条件的结论即可,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
