题目内容
已知数列{an}的前n项的和Sn,点(n,Sn)在函数f(x)=2x2+4x图象上,
(1)求数列{an}的通项公式;
(2)若函数g(x)=2 -x,数列{bn}满足bn=g(n),记cn=an•bn,求数列{cn}前n项和Tn;
(3)是否存在实数λ,使得当x≤λ时,f(x)=-x2+4x-
≤0对任意n∈N*恒成立?若存在,求出最大的实数λ,若不存在,说明理由.
(1)求数列{an}的通项公式;
(2)若函数g(x)=2 -x,数列{bn}满足bn=g(n),记cn=an•bn,求数列{cn}前n项和Tn;
(3)是否存在实数λ,使得当x≤λ时,f(x)=-x2+4x-
| an |
| n+1 |
考点:数列与函数的综合,数列的求和
专题:等差数列与等比数列
分析:(1)要求数列的通项公式,当n大于等于2时可根据数列的前n项的和减去数列的前n-1项的和求出,然后把n=1代入验证;
(2)由函数g(x)=2 -x,数列{bn}满足bn=g(n)=2 -n,利用错位相减法可得数列{cn}前n项和Tn;
(3)假设存在实数λ,使得当x≤λ时,f(x)=-x2+4x-
≤0对任意n∈N*恒成立,即-x2+4x≤
对任意n∈N*恒成立,由
=4-
是递增数列,能推导出存在最大的实数λ=1,使得当x≤λ时,f(x)≤cn对任意n∈N*恒成立.
(2)由函数g(x)=2 -x,数列{bn}满足bn=g(n)=2 -n,利用错位相减法可得数列{cn}前n项和Tn;
(3)假设存在实数λ,使得当x≤λ时,f(x)=-x2+4x-
| an |
| n+1 |
| an |
| n+1 |
| an |
| n+1 |
| 2 |
| n+1 |
解答:
解:(1)由题意,Sn=2n2+4n,
当n=1时,a1=S1=6,
n≥2时,
an=Sn-Sn-1=(2n2+4n)-[2(n-1)2+4(n-1)]=4n+2,
当n=1时,a1=S1=4+2=6,也适合上式
∴数列{an}的通项公式为an=4n+2,n∈N*;
(2)∵函数g(x)=2 -x,
∴数列{bn}满足bn=g(n)=2 -n,
又∵cn=an•bn,
∴Tn=6×2-1+10×2-2+14×2-3+…+(4n+2)×2-n,…①,
∴
Tn=6×2-2+10×2-3+…+(4n-2)×2-n+(4n+2)×2-(n+1),…②,
①-②得:
Tn=6×2-1+4(2-2+2-3+…+2-n)-(4n+2)×2-(n+1)=5-(2n+5)(
)n,
∴Tn=10-(2n+5)(
)n-1,
(3)假设存在实数λ,使得当x≤λ时,f(x)=-x2+4x-
≤0对任意n∈N*恒成立,
即-x2+4x≤
对任意n∈N*恒成立,
∵an=4n+2,
∴cn=
=
=4-
是递增数列,
所以只要-x2+4x≤c1,即x2-4x+3≥0,
解得x≤1或x≥3.
所以存在最大的实数λ=1,使得当x≤λ时,f(x)≤cn对任意n∈N*恒成立.
当n=1时,a1=S1=6,
n≥2时,
an=Sn-Sn-1=(2n2+4n)-[2(n-1)2+4(n-1)]=4n+2,
当n=1时,a1=S1=4+2=6,也适合上式
∴数列{an}的通项公式为an=4n+2,n∈N*;
(2)∵函数g(x)=2 -x,
∴数列{bn}满足bn=g(n)=2 -n,
又∵cn=an•bn,
∴Tn=6×2-1+10×2-2+14×2-3+…+(4n+2)×2-n,…①,
∴
| 1 |
| 2 |
①-②得:
| 1 |
| 2 |
| 1 |
| 2 |
∴Tn=10-(2n+5)(
| 1 |
| 2 |
(3)假设存在实数λ,使得当x≤λ时,f(x)=-x2+4x-
| an |
| n+1 |
即-x2+4x≤
| an |
| n+1 |
∵an=4n+2,
∴cn=
| an |
| n+1 |
| 4n+2 |
| n+1 |
| 2 |
| n+1 |
所以只要-x2+4x≤c1,即x2-4x+3≥0,
解得x≤1或x≥3.
所以存在最大的实数λ=1,使得当x≤λ时,f(x)≤cn对任意n∈N*恒成立.
点评:本题考查数列的通项公式和前n项和公式的求法,考查数列不等式的应用,解题时要认真审题,注意错位相消法和等价转化思想的合理运用.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
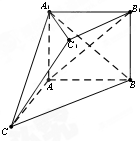 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,△A1BC是
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,△A1BC是