题目内容
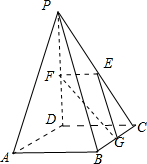
如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.(1)求证:平面PAB∥平面EFG;
(2)求直线EG与平面PAD所成角的余弦值;
(3)求平面EFG与平面ABCD所成的角.
(2)求直线EG与平面PAD所成角的余弦值;
(3)求平面EFG与平面ABCD所成的角.
考点:二面角的平面角及求法,平面与平面平行的判定,直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:(1)根据已知条件可得到EF∥AB,EG∥PB,所以EF∥平面PAB,EG∥平面PAB,所以平面PAB∥平面EFG;
(2)EG∥PB,所以EG与平面PAD所成角等于PB与平面PAD所成角,容易说明AB⊥平面PAD,所以∠APB是直线PB与平面PAD所成角,根据已知条件可求得PA,PB,所以该角的余弦值能够求出;
(3)根据(1)平面EFG∥平面PAB,所以平面EFG与平面ABCD所成的角等于平面PAB和平面ABCD所成角,并且容易找到平面PAB和平面ABCD所成角的平面角∠PAD,并且该角的值为45°.
(2)EG∥PB,所以EG与平面PAD所成角等于PB与平面PAD所成角,容易说明AB⊥平面PAD,所以∠APB是直线PB与平面PAD所成角,根据已知条件可求得PA,PB,所以该角的余弦值能够求出;
(3)根据(1)平面EFG∥平面PAB,所以平面EFG与平面ABCD所成的角等于平面PAB和平面ABCD所成角,并且容易找到平面PAB和平面ABCD所成角的平面角∠PAD,并且该角的值为45°.
解答:
解:(1)如图,由已知条件知:EF∥AB,AB?平面PAB,∴EF∥平面PAB,同理,EG∥平面PAB,EF∩EG=E;
 ∴平面EFG∥平面PAB,即平面PAB∥平面EFG;
∴平面EFG∥平面PAB,即平面PAB∥平面EFG;
(2)∵EG∥PB,∴EF与平面PAD所成角等于PB与平面PAD所成角;
∵PD⊥平面ABCD,AB?平面ABCD,∴PD⊥AB,即AB⊥PD,又AB⊥AD;
∴AB⊥平面PAD,∴∠APB是直线PB和平面PAD所成角;
∴在Rt△PAB中,AB=2,PA=2
,PB=
=2
;
∴cos∠APB=
=
=
;
∴直线EG与平面PAD所成角的余弦值为
;
(3)由(1)知平面EFG∥平面PAB,∴平面EFG与平面ABCD所成的角等于平面PAB与平面ABCD所成角;
由(2)知PA⊥AB,AD⊥AB;
∴∠PAD是平面PAB和平面ABCD所成二面角的平面角;
由已知条件知,PD=AD,PD⊥AD,∴∠PAD=45°;
∴平面EFG与平面ABCD所成的角为45°.
 ∴平面EFG∥平面PAB,即平面PAB∥平面EFG;
∴平面EFG∥平面PAB,即平面PAB∥平面EFG;(2)∵EG∥PB,∴EF与平面PAD所成角等于PB与平面PAD所成角;
∵PD⊥平面ABCD,AB?平面ABCD,∴PD⊥AB,即AB⊥PD,又AB⊥AD;
∴AB⊥平面PAD,∴∠APB是直线PB和平面PAD所成角;
∴在Rt△PAB中,AB=2,PA=2
| 2 |
| 12 |
| 3 |
∴cos∠APB=
| PA |
| PB |
2
| ||
2
|
| ||
| 3 |
∴直线EG与平面PAD所成角的余弦值为
| ||
| 3 |
(3)由(1)知平面EFG∥平面PAB,∴平面EFG与平面ABCD所成的角等于平面PAB与平面ABCD所成角;
由(2)知PA⊥AB,AD⊥AB;
∴∠PAD是平面PAB和平面ABCD所成二面角的平面角;
由已知条件知,PD=AD,PD⊥AD,∴∠PAD=45°;
∴平面EFG与平面ABCD所成的角为45°.
点评:考查中位线的性质,线面平行的判定定理,面面平行的判定定理,线面角的定义,以及二面角、二面角的平面角的概念.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
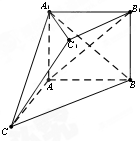 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,△A1BC是
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,△A1BC是