题目内容
已知椭圆E:
+
=1(a>b>0)的左、右焦点分别为F1、F2、A为上顶点,AF1交椭圆E于另一点B,且△ABF2的周长为8,离心率e=
.
(1)求椭圆E的标准方程;
(2)求过D(1,0)作椭圆E的两条互相垂直的弦,M,N分别为两弦的中点,求证:直线MN经过x轴上的定点,并求出定点的坐标.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆E的标准方程;
(2)求过D(1,0)作椭圆E的两条互相垂直的弦,M,N分别为两弦的中点,求证:直线MN经过x轴上的定点,并求出定点的坐标.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)AB+AF2+BF2=(AF1+AF2)+(BF1+BF2)=4a=8⇒a=2,再由离心率e=
,求出c,可得b,从而可以求出椭圆E的标准方程;
(2)由题设条件可知M,N的坐标,从而可得直线MN的方程,由此可推导出直线MN过定点.
| ||
| 2 |
(2)由题设条件可知M,N的坐标,从而可得直线MN的方程,由此可推导出直线MN过定点.
解答:
解:(1)AB+AF2+BF2=(AF1+AF2)+(BF1+BF2)=4a=8,∴a=2
∵离心率e=
,∴c=
,
∴b=
∴椭圆E的标准方程:
+
=1.
(2)设以M为中点的弦x=my+1与椭圆交于(x1,y1),(x2,y2),则
x=my+1代入
+
=1可得(m2+2)y2+2my-3=0,
x1+x2=m(y1+y2)+2=
∴M(
,-
),
同理N(
,
),
∴kMN=
,MN:y+
=
(x-
),
整理得y=
(x-
),
∴直线MN过定点(
,0).
当直线P1Q1的斜率不存在或为零时,P1Q1、P2Q2的中点为点D及原点O,直线MN为x轴,也过此定点,
∴直线MN过定点(
,0).
∵离心率e=
| ||
| 2 |
| 2 |
∴b=
| 2 |
∴椭圆E的标准方程:
| x2 |
| 4 |
| y2 |
| 2 |
(2)设以M为中点的弦x=my+1与椭圆交于(x1,y1),(x2,y2),则
x=my+1代入
| x2 |
| 4 |
| y2 |
| 2 |
x1+x2=m(y1+y2)+2=
| 4 |
| m2+2 |
∴M(
| 2 |
| m2+2 |
| m |
| m2+2 |
同理N(
| 2m2 |
| 2m2+1 |
| m |
| 2m2+1 |
∴kMN=
| 3m |
| 2(m2-1) |
| m |
| m2+2 |
| 3m |
| 2(m2-1) |
| 2 |
| m2+2 |
整理得y=
| 3m |
| 2(m2-1) |
| 2 |
| 3 |
∴直线MN过定点(
| 2 |
| 3 |
当直线P1Q1的斜率不存在或为零时,P1Q1、P2Q2的中点为点D及原点O,直线MN为x轴,也过此定点,
∴直线MN过定点(
| 2 |
| 3 |
点评:本题主要考查直线、椭圆的基础知识,考查函数与方程思想,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
已知正三棱锥P-ABC的四个顶点都在半径为
的球面上,M,N分别为PA,AB的中点.若MN⊥CM,则球心到平面ABC的距离为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
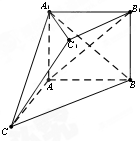 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,△A1BC是
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,△A1BC是 如图,平面α∥β∥γ,直线l、m分别与α、β、γ相交于点A、B、C和点D、E、F.若
如图,平面α∥β∥γ,直线l、m分别与α、β、γ相交于点A、B、C和点D、E、F.若