题目内容
已知函数f（x）=x2+（m2-4）x+m是偶函数，g（x）=xm在（-∞，0）内单调递增，则实数m=（ ）
| A、2 | B、±2 | C、0 | D、-2 |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：根据函数的奇偶性的性质求出m，结合幂函数的性质即可得到结论．
解答：
解：∵函数f（x）=x2+（m2-4）x+m是偶函数，
∴f（-x）=f（x），
即f（-x）=x2-（m2-4）x+m=x2+（m2-4）x+m，
则-（m2-4）=m2-4，
解得m2-4=0，解得m=2或-2，
∵若m=2，g（x）=x2在（-∞，0）内单调递减，不满足条件，
若m=-2，g（x）=x-2在（-∞，0）内单调递增，满足条件，
故选：D
∴f（-x）=f（x），
即f（-x）=x2-（m2-4）x+m=x2+（m2-4）x+m，
则-（m2-4）=m2-4，
解得m2-4=0，解得m=2或-2，
∵若m=2，g（x）=x2在（-∞，0）内单调递减，不满足条件，
若m=-2，g（x）=x-2在（-∞，0）内单调递增，满足条件，
故选：D
点评：本题主要考查函数奇偶性的应用以及幂函数的性质，比较基础．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
相关题目
已知|
|=|
|=2，
在
上的投影为-1，则向量
与向量
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、150° | B、120° |
| C、60° | D、30° |
一个四面体的三视图如图所示，则该四面体的外接球的表面积为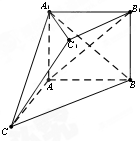
如图，在多面体ABC-A1B1C1中，四边形ABB1A1是正方形，AC=AB=1，△A1BC是