题目内容
已知点P(6,-4),圆C:x2+y2=20.
(1)求过点P及圆心C的直线方程;
(2)求过点P且在圆C中截出长为6
的弦所在直线方程.
(1)求过点P及圆心C的直线方程;
(2)求过点P且在圆C中截出长为6
| 2 |
考点:直线与圆相交的性质
专题:计算题,直线与圆
分析:(1)C(0,0),利用点斜式,可求过点P及圆心C的直线方程;
(2)设出直线的斜率写出直线方程,然后求出圆心到直线的距离d,因为圆的半弦长、半径、弦心距恰好构成Rt△,根据勾股定理列出方程求出k的值代入弦所在的直线方程即可.
(2)设出直线的斜率写出直线方程,然后求出圆心到直线的距离d,因为圆的半弦长、半径、弦心距恰好构成Rt△,根据勾股定理列出方程求出k的值代入弦所在的直线方程即可.
解答:
解:(1)由题意,C(0,0),
∴过点P及圆心C的直线方程为y=-
x;
(2)∵在圆C中截出长为6
,
∴圆心到直线的距离为
=
,
设直线方程为y+4=k(x-6),即kx-y-6k-4=0,
∴
=
,解得k=-
或k=-1.
∴直线方程为7x+17y+26=0或x+y-2=0.
∴过点P及圆心C的直线方程为y=-
| 2 |
| 3 |
(2)∵在圆C中截出长为6
| 2 |
∴圆心到直线的距离为
| 20-18 |
| 2 |
设直线方程为y+4=k(x-6),即kx-y-6k-4=0,
∴
| |-6k-4| | ||
|
| 2 |
| 7 |
| 17 |
∴直线方程为7x+17y+26=0或x+y-2=0.
点评:此题是一道直线与圆的方程的综合应用题,要求学生掌握点到直线的距离公式和勾股定理的应用,以及会根据条件写出直线的一般式方程.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
已知正三棱锥P-ABC的四个顶点都在半径为
的球面上,M,N分别为PA,AB的中点.若MN⊥CM,则球心到平面ABC的距离为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
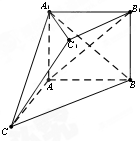 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,△A1BC是
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,△A1BC是