题目内容
1.椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$,过左焦点F1的直线交椭圆与A,B两点,则△ABF2的周长为( )| A. | 32 | B. | 20 | C. | 16 | D. | 12 |
分析 根据椭圆的定义即可得出答案.
解答 解:∵椭圆方程为$\frac{x^2}{16}+\frac{y^2}{9}=1$,∴a=4.
△ABF2的周长为AB+AF2+BF2=AF1+AF2+BF1+BF2=4a=16.
故选:C.
点评 本题考查了椭圆的定义与性质,属于基础题.

练习册系列答案
相关题目
16.已知命题p:“$\frac{x}{y}$>1”,命题q:“x>y”,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.已知集合A={x|2x>1},B={x|x2-3x-4>0},则∁R(A∪B)=( )
| A. | {x|x≤0或x>4} | B. | {x|x<-1或x>4} | C. | R | D. | {x|-1≤x≤0} |
13.方程($\frac{1}{3}$)x-x=0的解有( )
| A. | 0个 | B. | 3个 | C. | 2个 | D. | 1个 |
10.为了考察某种药物治疗效果,进行动物试验,得到如下数据:
(1)求出表格中b,c,d的值;
(2)是否有95%的把握认为该药物有效.
附:
i:${k^2}=\frac{{n{{(ad-bc)}^2}}}{{({a+b})({a+d})({b+c})({b+d})}}$
ii:
| 患病 | 未患病 | 总计 | |
| 服用药 | 10 | b | 50 |
| 未服药 | c | d | 50 |
| 总计 | 30 | 70 | 100 |
(2)是否有95%的把握认为该药物有效.
附:
i:${k^2}=\frac{{n{{(ad-bc)}^2}}}{{({a+b})({a+d})({b+c})({b+d})}}$
ii:
| P(k2≥k) | 0.15 | 0.05 | 0.025 | 0.005 |
| k | 2.072 | 3.841 | 5.024 | 7.879 |
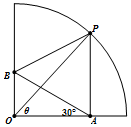 现有四分之一圆形的纸板(如图),∠AOB=90°,圆半径为1,要裁剪成四边形OAPB,且满足AP∥OB,∠OAB=30°,∠POA=θ,记此四边形OAPB的面积为f(θ),求f(θ)的最大值.
现有四分之一圆形的纸板(如图),∠AOB=90°,圆半径为1,要裁剪成四边形OAPB,且满足AP∥OB,∠OAB=30°,∠POA=θ,记此四边形OAPB的面积为f(θ),求f(θ)的最大值.