题目内容
16.某园林基地培育了一种新观赏植物,经过了一年的生长发育,技术人员从中抽取了部分植株的高度(单位:厘米)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]分组做出频率分布直方图,并作出样本高度的茎叶图(图中仅列出了高度在[50,60),[90,100]的数据).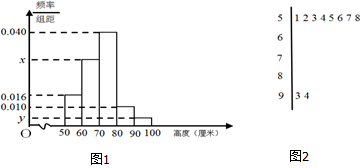
(1)求样本容量n和频率分布直方图中的x,y
(2)在选取的样本中,从高度在80厘米以上(含80厘米)的植株中随机抽取3株,设随机变量X表示所抽取的3株高度在[80,90)内的株数,求随机变量X的分布列及数学期望.
分析 (1)由茎叶图及频率分布直方图能求出样本容量n和频率分布直方图中的x,y.
(2)由题意可知,高度在[80,90)内的株数为5,高度在[90,100]内的株数为2,共7株.抽取的3株中高度在[80,90)内的株数X的可能取值为1,2,3,分别求出相应的概率,由此能求出X的分布列和E(X).
解答 解:(1)由题意可知,
样本容量$n=\frac{8}{0.016×10}=50,y=\frac{2}{50×10}=0.004$,
x=0.100-0.004-0.010-0.016-0.040=0.030.(4分)
(2)由题意可知,高度在[80,90)内的株数为5,高度在[90,100]内的株数为2,
共7株.抽取的3株中高度在[80,90)内的株数X的可能取值为1,2,3,(5分)
则P(X=1)=$\frac{{C}_{5}^{1}{C}_{2}^{2}}{{C}_{7}^{3}}$=$\frac{1}{7}$,
$P(X=2)=\frac{C_5^2C_2^1}{C_7^3}=\frac{20}{35}=\frac{4}{7}$,
$P(X=3)=\frac{C_5^3C_2^0}{C_7^3}=\frac{10}{35}=\frac{2}{7}$,(8分)
∴X的分布列为:
| X | 1 | 2 | 3 |
| P | $\frac{1}{7}$ | $\frac{4}{7}$ | $\frac{2}{7}$ |
故E(X)=$1×\frac{1}{7}+2×\frac{4}{7}+3×\frac{2}{7}$=$\frac{15}{7}$.(12分)
点评 本题考查概率的求法,考查离散型随机变量的分布列及数学期望的求法,涉及到平均数、方差、离散型随机变量的分布列及数学期望等知识点,考查推理论证能力、运算求解能力、数据处理能力,考查化归与转化思想,是中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目