题目内容
12.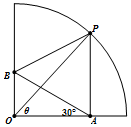 现有四分之一圆形的纸板(如图),∠AOB=90°,圆半径为1,要裁剪成四边形OAPB,且满足AP∥OB,∠OAB=30°,∠POA=θ,记此四边形OAPB的面积为f(θ),求f(θ)的最大值.
现有四分之一圆形的纸板(如图),∠AOB=90°,圆半径为1,要裁剪成四边形OAPB,且满足AP∥OB,∠OAB=30°,∠POA=θ,记此四边形OAPB的面积为f(θ),求f(θ)的最大值.
分析 利用已知条件列出梯形的面积的表达式,利用三角函数的最值求法求解即可.
解答 解:∵在直角梯形OAPB中,有AP=sinθ,OA=cosθ,$OB=\frac{{\sqrt{3}}}{3}cosθ$
∴${S_{OAPB}}=\frac{1}{2}(|{OB}|+|{AP}|)•|{OA}|=\frac{1}{2}(\frac{{\sqrt{3}}}{3}cosθ+sinθ)•cosθ$-----(4分)
=$\frac{1}{2}(\frac{{\sqrt{3}}}{3}{cos^2}θ+sinθ•cosθ)=\frac{1}{2}(\frac{{\sqrt{3}}}{3}\frac{1+cos2θ}{2}+\frac{1}{2}sin2θ)$=$\frac{{\sqrt{3}}}{6}sin(2θ+\frac{π}{6})+\frac{{\sqrt{3}}}{12}$.-----(8分)
又∵$0<θ<\frac{π}{2}$,则$\frac{π}{6}<2θ+\frac{π}{6}<\frac{7π}{6}$,
∴当且仅当$2θ+\frac{π}{6}=\frac{π}{2}$即$θ=\frac{π}{6}$时,面积取得最大值$\frac{{\sqrt{3}}}{4}$.(12分)
点评 本题考查实际问题的处理方法,三角函数的最值的应用,考查转化思想以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.春节期间,受烟花爆竹集中燃放影响,我国多数城市空气中PM2.5浓度快速上升,特别是在大气扩散条件不利的情况下,空气质量在短时间内会迅速恶化.2017年除夕18时和初一2时,国家环保部门对8个城市空气中PM2.5浓度监测的数据如表(单位:微克/立方米).
(Ⅰ)求这8个城市除夕18时空气中PM2.5浓度的平均值;
(Ⅱ)环保部门发现:除夕18时到初一2时空气中PM2.5浓度上升不超过100的城市都是“禁止燃放烟花爆竹“的城市,浓度上升超过100的城市都未禁止燃放烟花爆竹.从以上8个城市中随机选取3个城市组织专家进行调研,记选到“禁止燃放烟花爆竹”的城市个数为X,求随机变量y的分布列和数学期望;
(Ⅲ) 记2017年除夕18时和初一2时以上8个城市空气中PM2.5浓度的方差分别为s12和s22,比较s12和s22的大小关系(只需写出结果).
| 除夕18时PM2.5浓度 | 初一2时PM2.5浓度 | |
| 北京 | 75 | 647 |
| 天津 | 66 | 400 |
| 石家庄 | 89 | 375 |
| 廊坊 | 102 | 399 |
| 太原 | 46 | 115 |
| 上海 | 16 | 17 |
| 南京 | 35 | 44 |
| 杭州 | 131 | 39 |
(Ⅱ)环保部门发现:除夕18时到初一2时空气中PM2.5浓度上升不超过100的城市都是“禁止燃放烟花爆竹“的城市,浓度上升超过100的城市都未禁止燃放烟花爆竹.从以上8个城市中随机选取3个城市组织专家进行调研,记选到“禁止燃放烟花爆竹”的城市个数为X,求随机变量y的分布列和数学期望;
(Ⅲ) 记2017年除夕18时和初一2时以上8个城市空气中PM2.5浓度的方差分别为s12和s22,比较s12和s22的大小关系(只需写出结果).
8.已知全集为R,且A={x|log2(x+1)<2},B={x|$\frac{x-2}{x-1}$≥0},则A∩(∁RB)等于( )
| A. | (-1,1) | B. | (-1,1] | C. | [1,2] | D. | [1,2) |
5.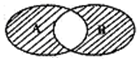 如图所示的韦恩图中,A、B是非空集合,定义A*B表示阴影部分的集合.若x,y∈R,A={x|y=$\sqrt{2x-{x}^{2}}$},B={y|y=3x,x>0}.则A*B为( )
如图所示的韦恩图中,A、B是非空集合,定义A*B表示阴影部分的集合.若x,y∈R,A={x|y=$\sqrt{2x-{x}^{2}}$},B={y|y=3x,x>0}.则A*B为( )
 如图所示的韦恩图中,A、B是非空集合,定义A*B表示阴影部分的集合.若x,y∈R,A={x|y=$\sqrt{2x-{x}^{2}}$},B={y|y=3x,x>0}.则A*B为( )
如图所示的韦恩图中,A、B是非空集合,定义A*B表示阴影部分的集合.若x,y∈R,A={x|y=$\sqrt{2x-{x}^{2}}$},B={y|y=3x,x>0}.则A*B为( )| A. | {x|0<x<2} | B. | {x|1<x≤2} | C. | {x|0≤x≤1或x≥2} | D. | {x|0≤x≤1或x>2} |
17.函数f(x)=x-sinx(x∈R),则f(x)( )
| A. | 是奇函数,且在(-∞,+∞)上是减函数 | B. | 是偶函数,且在(-∞,+∞)上是减函数 | ||
| C. | 是偶函数,且在(-∞,+∞)上是增函数 | D. | 是奇函数,且在(-∞,+∞)上是增函数 |
2.将4名学生分别安排甲、乙、丙三个地方参加实践活动,每个地方至少安排一名学生,则不同的安排方案共有( )
| A. | 12 | B. | 18 | C. | 24 | D. | 36 |