题目内容
6.我们知道,如果定义在某区间上的函数f(x)满足对该区间上的任意两个数x1,x2,总有不等式$\frac{{f({x_1})+f({x_2})}}{2}≤f({\frac{{{x_1}+{x_2}}}{2}})$成立,则称函数f(x)在该区间上的向上凸函数(简称上凸).类比上述定义,对于数列{an},如果对任意正整数n,总有不等式$\frac{{{a_n}+{a_{n+2}}}}{2}≤{a_{n+1}}$成立,则称数列{an}为向上凸数列(简称上凸数列),现有数列{an}满足如下两个条件:①数列{an}为上凸数列,且a1=1,a10=28;
②对正整数n(1≤n<10,n∈N*),都有|an-bn|≤20,其中${b_n}={n^2}-6n+10$,则数列{an}中的第三项a3的取值范围为[7,19].
分析 根据数列{an}为上凸数列,且a1=1,a10=28,求出a3≥7…①.根据正整数n(1≤n<10,n∈N*),都有|an-bn|≤20,求出19≤a3≤19…②.问题得以解决
解答 解:∵$\frac{{{a_n}+{a_{n+2}}}}{2}≤{a_{n+1}}$,
∴an+an+2≤2an+1,
∴an+an+2≤2an+1,
∴an+2-an+1≤an+1-an,
∴$\frac{{a}_{n+2}-{a}_{n+1}}{(n+2)-(n+1)}$≤$\frac{{a}_{n+1}-{a}_{n}}{(n+1)-n}$,
∴$\frac{{a}_{10}-{a}_{1}}{10-1}$≤$\frac{{a}_{3}-{a}_{1}}{3-1}$
把a1=1,a10=28代入,得a3≥7…①.
在|an-bn|≤20,bn=n2-6n+10中,令n=3,得b3=9-18+10=1,
∴-20≤a3-b3≤20,
∴-19≤a3≤19…②.
①②联立得7≤a3≤19.
故答案为:[7,19].
点评 本题新定义的学习和应用,考查了学生的转化能力和运算能力,属于中档题

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
17.函数f(x)=x-sinx(x∈R),则f(x)( )
| A. | 是奇函数,且在(-∞,+∞)上是减函数 | B. | 是偶函数,且在(-∞,+∞)上是减函数 | ||
| C. | 是偶函数,且在(-∞,+∞)上是增函数 | D. | 是奇函数,且在(-∞,+∞)上是增函数 |
15.下列函数中,以π为最小正周期的偶函数,且在(0,$\frac{π}{4}$)上单调递增的函数是( )
| A. | y=sinx | B. | y=sin2|x| | C. | y=-cos2x | D. | y=cos2x |
 如果执行右边的程序框图,输出的值为x,则${x}^{\frac{1}{2}}$+log3x=5.
如果执行右边的程序框图,输出的值为x,则${x}^{\frac{1}{2}}$+log3x=5.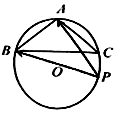 如图,在△A BC中,三内角 A,B,C的对边分别为a,b,c,且a2=b2+c2+bc,$a=\sqrt{3}$,S为△A BC的面积,圆 O是△A BC的外接圆,P是圆 O上一动点,
如图,在△A BC中,三内角 A,B,C的对边分别为a,b,c,且a2=b2+c2+bc,$a=\sqrt{3}$,S为△A BC的面积,圆 O是△A BC的外接圆,P是圆 O上一动点,