题目内容
函数f(x)=
的定义域为 .(用区间表示)
| ||
| ln(-x2+4x-3) |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:由对数函数的性质知函数的真数>0,分母不为0,同时2x-3≥0,由此能求出结果.
解答:
解:函数f(x)=
的应满足:
解得
≤x<2,或2<x<3.
故答案为:[
,2)∪(2,3).
| ||
| ln(-x2+4x-3) |
|
解得
| 3 |
| 2 |
故答案为:[
| 3 |
| 2 |
点评:本题考查对数函数的定义域,解题时要认真审题,注意对数的真数要大于0.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
已知△ABC中,三个内角A,B,C的对边分别为a,b,c,若asinA-csinC=(a-b)sinB,则角C为( )
| A、60° | B、30° |
| C、120° | D、150° |
已知数列an=8+
若其最大项和最小项分别为M和m,则m+M的值为( )
| 2n-7 |
| 2n |
A、
| ||
B、
| ||
C、
| ||
D、
|
方程4x-2x+1+4m=0只有一个实数解,则实数m的取值范围是( )
| A、{m|m≤0} | ||
B、{m|0<m<
| ||
C、{m|m>
| ||
D、{m|m≤0或m=
|
 如图,设双曲线
如图,设双曲线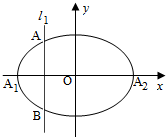 如图,椭圆Γ:
如图,椭圆Γ: