题目内容
已知直线x=1是函数f(x)的图象的一条对称轴,对任意x∈R,f(x+2)=-f(x),当-1≤x≤1时,f(x)=x3,求f(x)在R上的解析式.
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:根据题意,求出f(x)是周期为4的函数,再求出函数f(x)在x∈[1,3]时的解析式,
即得f(x)在一个周期内的解析式,从而得出函数f(x)在R上的解析式.
即得f(x)在一个周期内的解析式,从而得出函数f(x)在R上的解析式.
解答:
解:∵x=1是f(x)的图象的一条对称轴,∴f(x+2)=f(-x);
又∵f(x+2)=-f(x),∴f(x)=-f(x+2)=-f(-x),
即f(-x)=-f(x);
∴f(x)是奇函数;
又∵f(x+2)=-f(x),
∴f(x+4)=f[(x+2)+2]=-f(x+2)=f(x),
∴函数的周期是T=4;
当x∈[1,3]时,x-2∈[-1,1],
又∵当-1≤x≤1时,f(x)=x3,
∴f(x-2)=(x-2)3,
∴f(x)=f[(x-2)+2]=-f(x-2)=-(x-2)3,
∴当x∈[1,3]时,f(x)=-(x-2)3;
∴当x∈[-1,3]时,f(x)=
;
又∵函数f(x)的周期为4,
∴当x∈R时,f(x)=
,k∈Z.
又∵f(x+2)=-f(x),∴f(x)=-f(x+2)=-f(-x),
即f(-x)=-f(x);
∴f(x)是奇函数;
又∵f(x+2)=-f(x),
∴f(x+4)=f[(x+2)+2]=-f(x+2)=f(x),
∴函数的周期是T=4;
当x∈[1,3]时,x-2∈[-1,1],
又∵当-1≤x≤1时,f(x)=x3,
∴f(x-2)=(x-2)3,
∴f(x)=f[(x-2)+2]=-f(x-2)=-(x-2)3,
∴当x∈[1,3]时,f(x)=-(x-2)3;
∴当x∈[-1,3]时,f(x)=
|
又∵函数f(x)的周期为4,
∴当x∈R时,f(x)=
|
点评:本题考查了函数的周期性与奇偶性的应用问题,也考查了分段函数的解析式的问题以及函数的对称性问题,是综合性题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若2x=8Y+1且9y=3x-9,则x+y的值是( )
| A、18 | B、24 | C、21 | D、27 |
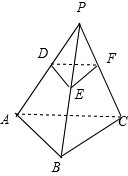 如图,已知点P为△ABC所在平面外任一点点D、E、F分别在射线PA、PB、PC上并且
如图,已知点P为△ABC所在平面外任一点点D、E、F分别在射线PA、PB、PC上并且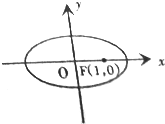 已知椭圆
已知椭圆