题目内容
已知数列an=8+
若其最大项和最小项分别为M和m,则m+M的值为( )
| 2n-7 |
| 2n |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列的函数特性
专题:函数的性质及应用,不等式的解法及应用
分析:运用函数求解解析式判断n→+∞时,an→8,a1=
,最小项为
,运用不等式
即
得出a5=
为最大项,求解即可.
| 11 |
| 2 |
| 11 |
| 2 |
|
即
|
| 259 |
| 32 |
解答:
解:∵数列an=8+
,
∴若其最大项为n项,则
即
∵n∈N,
∴n=5,a5=
为最大项,
n→+∞时,an→8,
∵a1=
∴最小项为
,
∴m+M的值为
+
=
故选:D
| 2n-7 |
| 2n |
∴若其最大项为n项,则
|
即
|
|
∵n∈N,
∴n=5,a5=
| 259 |
| 32 |
n→+∞时,an→8,
∵a1=
| 11 |
| 2 |
∴最小项为
| 11 |
| 2 |
∴m+M的值为
| 11 |
| 2 |
| 259 |
| 32 |
| 435 |
| 32 |
故选:D
点评:本题考查了函数的思想,不等式的性质,运用极限思想判断最大值,最小值,属于中档题.

练习册系列答案
相关题目
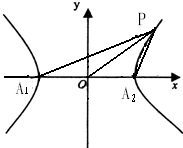 如图,P是双曲线
如图,P是双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、(0,
| ||
B、(0,
| ||
C、(0,
| ||
D、(0,
|
sin21°+sin22°+sin23°+sin288°+sin289°+sin290°=( )
| A、45 | ||||
B、45
| ||||
C、
| ||||
D、
|