题目内容
18.已知f(x)=2x,若$p=f({\sqrt{ab}})$,$q=f({\frac{a+b}{2}})$,$r=\frac{1}{2}({f(a)+f(b)})$,其中,a>b>0,则下列关系中正确的是( )| A. | p<r<q | B. | q<p<r | C. | r<p<q | D. | p<q<r |
分析 由题意可得p=${2}^{\sqrt{ab}}$,q=${2}^{\frac{a+b}{2}}$>${2}^{\sqrt{ab}}$=p,r=$\frac{1}{2}$(2a+2b)>${2}^{\sqrt{ab}}$,可得大小关系.
解答 解:∵f(x)=2x,a>b>0,
∴p=${2}^{\sqrt{ab}}$,
q=${2}^{\frac{a+b}{2}}$>${2}^{\sqrt{ab}}$=p,
r=$\frac{1}{2}$(2a+2b)${2}^{\frac{a+b}{2}}$>${2}^{\sqrt{ab}}$,
∴p<q<r,
故选:D.
点评 本题考查不等式与不等关系,涉及基本不等式和对数的运算,属基础题.

练习册系列答案
相关题目
9.已知四面体ABCD,$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DB}$=$\overrightarrow{b}$,$\overrightarrow{DC}$=$\overrightarrow{c}$,点M在棱DA上,$\overrightarrow{DM}$=2$\overrightarrow{MA}$,N为BC中点,则$\overrightarrow{MN}$=( )
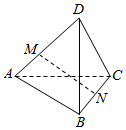

| A. | -$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ | B. | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
3.已知圆锥的母线长是10,侧面展开图是半圆,则该圆锥的侧面积为( )
| A. | $\frac{100}{3}$π | B. | 100π | C. | $\frac{50}{3}$π | D. | 50π |
7.已知[t]表示不超过t的最大整数,例如[1.25]=1,[2]=2,若关于x的方程$\frac{[x]}{x-1}$=a在(1,+∞)恰有2个不同的实数解,则实数a的取值范围是( )
| A. | [2,+∞) | B. | (2,+∞) | C. | ($\frac{3}{2}$,2] | D. | [$\frac{3}{2}$,2] |