题目内容
8.已知△ABC三个顶点的坐标分别为A(2,0),B(7,0),C(1,2),D为BC的中点.(Ⅰ)求AD所在直线的方程;
(Ⅱ)求△ACD外接圆的方程.
分析 (Ⅰ)求出D的坐标,利用两点式求AD所在直线的方程;
(Ⅱ)利用待定系数法求△ACD外接圆的方程.
解答 解:(Ⅰ)由题意,D(4,1),
∵A(2,0),
∴AD所在直线的方程为$\frac{y-0}{x-2}$=$\frac{1-0}{4-2}$,即x-2y-2=0;
(Ⅱ)设△ACD外接圆的方程为x2+y2+Dx+Ey+F=0,
A,C,D代入可得$\left\{\begin{array}{l}{2D+F+4=0}\\{D+2E+F+5=0}\\{4D+E+F+17=0}\end{array}\right.$,∴D=-5,E=-3,F=6,
∴△ACD外接圆的方程为x2+y2-5x-3y+6=0.
点评 本题考查直线方程,考查三角形外接圆的方程的求法,是基础题,解题时要认真审题,注意待定系数法的合理运用.

练习册系列答案
相关题目
3.设a=21.2,b=log38,c=0.83.1,则( )
| A. | b<a<c | B. | c<a<b | C. | c<b<a | D. | a<c<b |
20.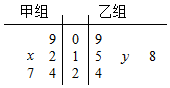 如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为18,乙组数据的中位数为16,则x,y的值分别为( )
如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为18,乙组数据的中位数为16,则x,y的值分别为( )
 如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为18,乙组数据的中位数为16,则x,y的值分别为( )
如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为18,乙组数据的中位数为16,则x,y的值分别为( )| A. | 18,6 | B. | 8,16 | C. | 8,6 | D. | 18,16 |
17.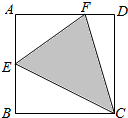 如图,四边形ABCD为正方形,E为AB的中点,F为AD上靠近D的三等分点,若向正方形内随机投掷一个点,则该点落在△CEF内的概率为( )
如图,四边形ABCD为正方形,E为AB的中点,F为AD上靠近D的三等分点,若向正方形内随机投掷一个点,则该点落在△CEF内的概率为( )
 如图,四边形ABCD为正方形,E为AB的中点,F为AD上靠近D的三等分点,若向正方形内随机投掷一个点,则该点落在△CEF内的概率为( )
如图,四边形ABCD为正方形,E为AB的中点,F为AD上靠近D的三等分点,若向正方形内随机投掷一个点,则该点落在△CEF内的概率为( )| A. | $\frac{9}{16}$ | B. | $\frac{7}{16}$ | C. | $\frac{7}{12}$ | D. | $\frac{5}{12}$ |
18.已知f(x)=2x,若$p=f({\sqrt{ab}})$,$q=f({\frac{a+b}{2}})$,$r=\frac{1}{2}({f(a)+f(b)})$,其中,a>b>0,则下列关系中正确的是( )
| A. | p<r<q | B. | q<p<r | C. | r<p<q | D. | p<q<r |
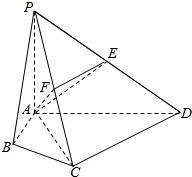 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.