题目内容
7.已知[t]表示不超过t的最大整数,例如[1.25]=1,[2]=2,若关于x的方程$\frac{[x]}{x-1}$=a在(1,+∞)恰有2个不同的实数解,则实数a的取值范围是( )| A. | [2,+∞) | B. | (2,+∞) | C. | ($\frac{3}{2}$,2] | D. | [$\frac{3}{2}$,2] |
分析 化为解y=[x]与y=a(x-1)在(1,+∞)上恰有2个不同的交点,从而作图求解即可.
解答 解:∵关于x的方程$\frac{[x]}{x-1}$=a在(1,+∞)恰有2个不同的实数解,
∴y=[x]与y=a(x-1)在(1,+∞)上恰有2个不同的交点,
作函数y=[x]与y=a(x-1)在(1,+∞)上的图象如下, ,
,
结合图象可知,kl=2,km=$\frac{3}{2}$,
实数a的取值范围是($\frac{3}{2}$,2],
故选C.
点评 本题考查了方程的解与函数的图象的关系应用及数形结合的思想应用.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
17.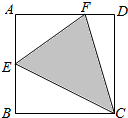 如图,四边形ABCD为正方形,E为AB的中点,F为AD上靠近D的三等分点,若向正方形内随机投掷一个点,则该点落在△CEF内的概率为( )
如图,四边形ABCD为正方形,E为AB的中点,F为AD上靠近D的三等分点,若向正方形内随机投掷一个点,则该点落在△CEF内的概率为( )
 如图,四边形ABCD为正方形,E为AB的中点,F为AD上靠近D的三等分点,若向正方形内随机投掷一个点,则该点落在△CEF内的概率为( )
如图,四边形ABCD为正方形,E为AB的中点,F为AD上靠近D的三等分点,若向正方形内随机投掷一个点,则该点落在△CEF内的概率为( )| A. | $\frac{9}{16}$ | B. | $\frac{7}{16}$ | C. | $\frac{7}{12}$ | D. | $\frac{5}{12}$ |
18.已知f(x)=2x,若$p=f({\sqrt{ab}})$,$q=f({\frac{a+b}{2}})$,$r=\frac{1}{2}({f(a)+f(b)})$,其中,a>b>0,则下列关系中正确的是( )
| A. | p<r<q | B. | q<p<r | C. | r<p<q | D. | p<q<r |
2.函数f(x)=x2-($\frac{1}{2}$)|x|的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |