题目内容
13.已知向量$\overrightarrow m=({cosA,sinB}),\overrightarrow n=({cosB,-sinA})$,$\overrightarrow m•\overrightarrow n=-cos2C$,且A,B,C分别为△ABC的三边a,b,c所对的角.(I)求角C的大小;
(Ⅱ)若a+b=2c,且△ABC的面积为$15\sqrt{3}$,求c边的长.
分析 (Ⅰ)根据平面向量的数量积的运算法则及两角和的余弦函数公式化简,得到-cos2C等于-cosC,化简后即可求出cosC的值,根据C的范围,利用特殊角的三角函数值即可求出C的度数;
(Ⅱ)利用已知及三角形面积公式可求ab=60,结合已知利用余弦定理即可解得c的值.
解答 (本题满分为12分)
解:(I)∵$\overrightarrow m•\overrightarrow n=-cos2C$=cosAcosB-sinAsinB=cos(A+B)=-cosC,
∴-cos2C=-cosC,整理可得:2cos2C-cosC-1=0,
∴cosC=-$\frac{1}{2}$或1,
∵C∈(0,π),
∴C=$\frac{2π}{3}$…6分
(Ⅱ)S△ABC=$\frac{1}{2}$absinC=$\frac{1}{2}$absin$\frac{2π}{3}$=15$\sqrt{3}$,
∴ab=60,a+b=2c,
∵c2=a2+b2-2abcosC=(a+b)2-2ab(1+cosC)=20,
∴解得:c=2$\sqrt{5}$…12分
点评 本题主要考查了平面向量的数量积的运算,两角和的余弦函数公式,特殊角的三角函数值,三角形面积公式,余弦定理等知识在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.

练习册系列答案
相关题目
3.设a=21.2,b=log38,c=0.83.1,则( )
| A. | b<a<c | B. | c<a<b | C. | c<b<a | D. | a<c<b |
1.设全集U={x∈N|x≤8},集合A={1,3,7},B={2,3,8},则(∁UA)∩(∁UB)=( )
| A. | {1,2,7,8} | B. | {4,5,6} | C. | {0,4,5,6} | D. | {0,3,4,5,6} |
18.已知f(x)=2x,若$p=f({\sqrt{ab}})$,$q=f({\frac{a+b}{2}})$,$r=\frac{1}{2}({f(a)+f(b)})$,其中,a>b>0,则下列关系中正确的是( )
| A. | p<r<q | B. | q<p<r | C. | r<p<q | D. | p<q<r |
5.如果直线3ax+y-1=0与直线(1-2a)x+ay+1=0平行.那么a等于( )
| A. | -1 | B. | $\frac{1}{3}$ | C. | 3 | D. | -1或$\frac{1}{3}$ |
2.函数f(x)=x2-($\frac{1}{2}$)|x|的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
3.执行如图所示的程序框图,输出的结果是( )
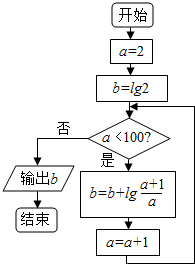

| A. | lg97 | B. | lg98 | C. | lg99 | D. | 2 |