题目内容

6．已知0＜θ＜π，tan（θ+$\frac{π}{4}$）=$\frac{1}{7}$，那么sinθ+cosθ=-$\frac{1}{5}$．

分析 由条件利用同角三角函数的基本关系，两角和的正切公式求得sinθ和cosθ的值，可得sinθ+cosθ的值．

解答 解：∵0＜θ＜π，$tan（θ+\frac{π}{4}）=\frac{1}{7}$=$\frac{tanθ+1}{1-tanθ}$，∴tanθ=-$\frac{3}{4}$=$\frac{sinθ}{cosθ}$，
再根据sinθ＞0，cosθ＜0，sin2θ+cos2θ=1，可得sinθ=$\frac{3}{5}$，cosθ=-$\frac{4}{5}$，
∴sinθ+cosθ=-$\frac{1}{5}$，
故答案为：$-\frac{1}{5}$．

点评 本题主要考查同角三角函数的基本关系，两角和的正切公式的应用，属于基础题．

练习册系列答案
相关题目
16．对a，b∈R，记max{a，b}=$\left\{\begin{array}{l}{a，a≥b}\\{b，a＞b}\end{array}\right.$，则函数f（x）=max{|x+1|，x+2}（x∈R）的最小值是$\frac{1}{2}$．
17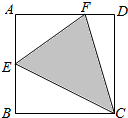．如图，四边形ABCD为正方形，E为AB的中点，F为AD上靠近D的三等分点，若向正方形内随机投掷一个点，则该点落在△CEF内的概率为（　　）
A．$\frac{9}{16}$B．$\frac{7}{16}$C．$\frac{7}{12}$D．$\frac{5}{12}$
14．函数f（x）=ax-1-2（a＞0，a≠1）的图象恒过定点A，若点A在直线mx-ny-1=0上，其中m＞0，n＞0，则$\frac{1}{m}+\frac{2}{n}$的最小值为（　　）
A．4B．5C．6D．$3+2\sqrt{2}$
1．设全集U={x∈N|x≤8}，集合A={1，3，7}，B={2，3，8}，则（∁UA）∩（∁UB）=（　　）
A．{1，2，7，8}B．{4，5，6}C．{0，4，5，6}D．{0，3，4，5，6}
11．偶函数f（x）=Asin（ωx+φ）（A≠0，ω＞0，0≤φ≤π）的图象向右平移$\frac{π}{4}$个单位得到的图象关于原点对称，则ω的值可以为（　　）
A．1B．2C．3D．4
18．已知f（x）=2x，若$p=f（{\sqrt{ab}}）$，$q=f（{\frac{a+b}{2}}）$，$r=\frac{1}{2}（{f（a）+f（b）}）$，其中，a＞b＞0，则下列关系中正确的是（　　）
A．p＜r＜qB．q＜p＜rC．r＜p＜qD．p＜q＜r
15．在平面直角坐标系中，以原点为极点，x轴的正半轴为极轴建立极坐标系，已知圆C的圆心C极坐标为（1，$\frac{π}{2}$），半径r=1．
（1）求圆C的极坐标方程；
（2）若α∈（0，$\frac{π}{2}$），直线l的参数方程为$\left\{\begin{array}{l}{x=1+tcosα}\\{y=2+tsinα}\end{array}\right.$（t为参数），点P的直角坐标为（1，2），直线l交圆C于A，B两点，求$\frac{|PA|•|PB|}{|PA|+|PB|}$的最小值．
16．已知函数f（x）=$\sqrt{|x+5|-|x-1|+t}$的定义域为R．
（1）求实数t的取值范围；
（2）若t的最小值为s，正实数a、b满足$\frac{2}{a+2b}$+$\frac{1}{2a+b}$=s，求4a+5b的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网