题目内容
9.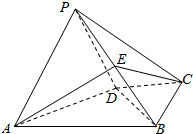 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,∠ABC=90°,AB=2,AD=$\sqrt{2}$,PA=PD=CD=CB=1,E总是线段PB上的动点.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,∠ABC=90°,AB=2,AD=$\sqrt{2}$,PA=PD=CD=CB=1,E总是线段PB上的动点.(Ⅰ)当E点在什么位置时,CE∥平面PAD?证明你的结论.
(Ⅱ)对于(Ⅰ)中的点E,求AE与底面ABCD所成角的正弦值;
(Ⅲ)求二面角A-PD-C的正弦值.
分析 (Ⅰ)取PA的中点F,连接DF,EF,由已知结合三角形中位线定理可得四边形DFEC是平行四边形,从而得到CE∥DF.再由线面平行的判定得答案;
(Ⅱ)由题意证明OA,OG,OP两两互相垂直,故以OA,OG,OP所在直线分别为x,y,z轴建立如图所示空间直角坐标系Oxyz.求出所用点的坐标,求得$\overrightarrow{AE}$的坐标,再求出底面ABCD的一个法向量,则AE与底面ABCD所成角的正弦值可求;
(Ⅲ)分别求出平面APD与平面PCD的一个法向量,求出两法向量所成角的余弦值,则二面角A-PD-C的正弦值可求.
解答  解:(Ⅰ)当E为PB的中点时,CE∥平面PAD.
解:(Ⅰ)当E为PB的中点时,CE∥平面PAD.
证明如下:取PA的中点F,连接DF,EF,则EF∥$\frac{1}{2}AB$,$EF=\frac{1}{2}AB$.
由已知CD$∥\frac{1}{2}AB$,CD=$\frac{1}{2}AB$,则EF∥CD,EF=CD.
∴四边形DFEC是平行四边形,∴CE∥DF.
又CE?平面PAD,DF?平面PAD,∴CE∥平面PAD;
(Ⅱ)取AD中点O,AB的中点G,连接OP,OG,
∵PA=PD,∴PO⊥AD,
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴PO⊥平面ABCD.
由已知可得AD2+BD2=AB2,∴BD⊥AD,
又OG∥BD,∴OG⊥AD,
∴OA,OG,OP两两互相垂直,
故以OA,OG,OP所在直线分别为x,y,z轴建立如图所示空间直角坐标系Oxyz.
A($\frac{\sqrt{2}}{2},0,0$),P(0,0,$\frac{\sqrt{2}}{2}$),B($-\frac{\sqrt{2}}{2},\sqrt{2},0$),E($-\frac{\sqrt{2}}{4},\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{4}$),
D($-\frac{\sqrt{2}}{2},0,0$),C($-\sqrt{2}$,$\frac{\sqrt{2}}{2}$,0).
∴$\overrightarrow{AE}=(-\frac{3\sqrt{2}}{4},\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{4})$,
$\overrightarrow{OP}=(0,0,\frac{\sqrt{2}}{2})$是平面ABCD的一个法向量,
设AE与底面ABCD所成角为θ,则
sinθ=|cos$<\overrightarrow{OP},\overrightarrow{AE}>$|=$\frac{|\overrightarrow{OP}•\overrightarrow{AE}|}{|\overrightarrow{OP}|•|\overrightarrow{AE}|}$=$\frac{\frac{1}{4}}{\frac{\sqrt{7}}{2}×\frac{\sqrt{2}}{2}}=\frac{\sqrt{14}}{14}$;
(Ⅲ)平面APD的一个法向量为$\overrightarrow{a}=(0,1,0)$,
$\overrightarrow{PD}=(-\frac{\sqrt{2}}{2},0,-$$\frac{\sqrt{2}}{2})$,$\overrightarrow{PC}$=($-\sqrt{2}$,$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$).
再设平面PCD的一个法向量为$\overrightarrow{b}=(x,y,z)$,
由$\left\{\begin{array}{l}{\overrightarrow{b}•\overrightarrow{PD}=0}\\{\overrightarrow{b}•\overrightarrow{PC}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{-\frac{\sqrt{2}}{2}x-\frac{\sqrt{2}}{2}z=0}\\{-\sqrt{2}x+\frac{\sqrt{2}}{2}y-\frac{\sqrt{2}}{2}z=0}\end{array}\right.$,
取z=1,则x=-1,y=-1,
∴$\overrightarrow{b}=(-1,-1,1)$.
∴二面角A-PD-C的余弦值的绝对值为$\frac{|\overrightarrow{a}•\overrightarrow{b}|}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$.
∴二面角A-PD-C的正弦值为$\frac{\sqrt{6}}{3}$.
点评 本题考查平面与平面垂直的性质,考查了利用空间向量求线面角和面面角,考查空间想象能力和思维能力,是中档题.

| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
| A. | “b2=ac”是“a,b,c成等比数列”的充要条件 | |
| B. | “?x∈R,x2>0”的否定是“?x0∈R,x02>0” | |
| C. | “若a=-4,则函数f(x)=ax2+4x-1只有唯一一个零点”的逆命题为真命题 | |
| D. | “函数f(x)=lnx2与函数g(x)=$\left\{\begin{array}{l}{2lnx,x>0}\\{2ln(-x),x<0}\end{array}\right.$的图象相同” |
| A. | 恒为正 | B. | 等于零 | C. | 恒为负 | D. | 不小于零 |
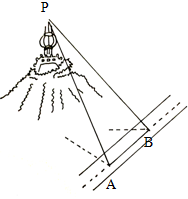 沿着山边一条平直的公路测量山顶一建筑物的高度,如图所示,已知A处测量建筑物顶部的仰角为60°,B处测量建筑物顶部的仰角为30°,已知图中
沿着山边一条平直的公路测量山顶一建筑物的高度,如图所示,已知A处测量建筑物顶部的仰角为60°,B处测量建筑物顶部的仰角为30°,已知图中