题目内容
18.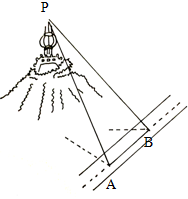 沿着山边一条平直的公路测量山顶一建筑物的高度,如图所示,已知A处测量建筑物顶部的仰角为60°,B处测量建筑物顶部的仰角为30°,已知图中
沿着山边一条平直的公路测量山顶一建筑物的高度,如图所示,已知A处测量建筑物顶部的仰角为60°,B处测量建筑物顶部的仰角为30°,已知图中PA⊥AB,AB=$\frac{440\sqrt{6}}{3}$米,山的高度是190米,则建筑物的高度为30 米.
分析 过P作PC⊥平面ABC,则利用直角三角形的性质和勾股定理得出各边的关系,列出方程解出.
解答  解:过P作PC⊥平面ABC,则∠PBC=30°,∠PAC=60°,∠PCB=∠PCA=90°.
解:过P作PC⊥平面ABC,则∠PBC=30°,∠PAC=60°,∠PCB=∠PCA=90°.
设PC=x,则PB=2x,AC=$\frac{x}{\sqrt{3}}$,PA=2AC=$\frac{2x}{\sqrt{3}}$,
∵PA⊥AB,∴PA2+AB2=PB2.即$\frac{4{x}^{2}}{3}+(\frac{440\sqrt{6}}{3})^{2}$=4x2.解得x=220.
∴建筑物的高度为220-190=30米.
故答案为30.
点评 本题考查了解三角形的应用,构造直角三角形是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.某变速运动的物体,路程s(米)随时间t(秒)变化的函数关系式是s=t2-2t+5,则此物体在t=1秒时的瞬时速度为( )
| A. | 2m/s | B. | 0m/s | C. | 4m/s | D. | -4m/s |
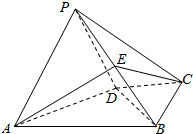 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,∠ABC=90°,AB=2,AD=$\sqrt{2}$,PA=PD=CD=CB=1,E总是线段PB上的动点.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,∠ABC=90°,AB=2,AD=$\sqrt{2}$,PA=PD=CD=CB=1,E总是线段PB上的动点.