函数$f(x)={log 3}x-{^x}$.若实数x0是函数f(x)的零点.且0＜x1＜x0.则f(x1)的值为( )A．恒为正B．等于零C．恒为负D．不小于零题目和参考答案——青夏教育精英家教网—

题目内容

19．函数$f（x）={log_3}x-{（\frac{1}{2}）^x}$，若实数x₀是函数f（x）的零点，且0＜x₁＜x₀，则f（x₁）的值为（　　）

A．

恒为正

B．

等于零

C．

恒为负

D．

不小于零

分析易知函数$f（x）={log_3}x-{（\frac{1}{2}）^x}$在（0，+∞）上是增函数且连续，再由f（x₀）=0且0＜x₁＜x₀判断即可．

解答解：易知函数$f（x）={log_3}x-{（\frac{1}{2}）^x}$在（0，+∞）上是增函数且连续，
∵实数x₀是函数f（x）的零点，
∴f（x₀）=0，
∵0＜x₁＜x₀，
∴f（x₁）＜f（x₀）=0，
故选：C．

点评本题考查了函数的单调性的判断与函数的连续性的判断，同时考查了函数的零点的应用．

练习册系列答案

相关题目

9．

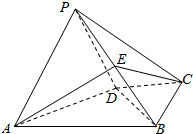如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，AB∥CD，∠ABC=90°，AB=2，AD=$\sqrt{2}$，PA=PD=CD=CB=1，E总是线段PB上的动点．
（Ⅰ）当E点在什么位置时，CE∥平面PAD？证明你的结论．
（Ⅱ）对于（Ⅰ）中的点E，求AE与底面ABCD所成角的正弦值；
（Ⅲ）求二面角A-PD-C的正弦值．

10．（1）实数a，b满足不等式组$\left\{\begin{array}{l}{b＞0}\\{a+b+1＜0}\\{3a+b+9＞0}\end{array}\right.$，则在坐标平面aOb内，点（a，b）对应的区域S，求目标函数z=2a-b的取值范围．
（2）过点（-5，1）的光线经x轴反射后的光线过区域S，求反射光线所在直线l经过区域S内的整点（即横纵坐标为整数的点）时直线l的方程．

7．设{a_n}是一个公差不为零的等差数列，其前n项和为S_n，已知S₉=90，且a₁，a₂，a₄成等比数列．
（1）求数列{a_n}的通项公式；
（2）设b_n=$\frac{1}{{{a_n}{a_{n+1}}}}$，求数列{b_n}的前n项和T_n．

14．函数f（x）=$\frac{1}{x^2}$+1的图象关于（　　）

4．不用计算器求下列各式的值．
（1）设${x^{\frac{1}{2}}}+{x^{-\frac{1}{2}}}$=3，求x+x^-1的值；
（2）若xlog₃4=1，求4^x+4^-x的值；
（3）[（1-log₆3）²+log₆2•log₆18]÷log₆4
（4）$\frac{1}{{\sqrt{2}-1}}-{（{\frac{3}{5}}）^0}+{（{\frac{9}{4}}）^{-0.5}}+\root{4}{{{{（\sqrt{2}-e）}^4}}}$．

11．函数f（x）=2a^x+1+3（a＞0且a≠1）的图象经过的定点坐标是（-1，5）．

8．求$\underset{lim}{x→0}$（$\frac{1}{x}$-cotx）．

11．在△ABC中，A：B=1：2，sinC=1，则a：b：c=（　　）

试题分类